Resampling Strategies

As future data scientists, you are probably well aware of the challenges involved in data collection — time, cost, and the complexities of experimental design often make large datasets hard to come by. However, robust predictive modeling is critical not only because extensive datasets can be rare, but also because ensuring that models generalize well to new data is often an essential question.

Resampling methods offer a powerful approach to assess model performance and mitigate overfitting. Rather than relying on a single train-test split, which can yield performance estimates that vary significantly depending on the split, resampling techniques repeatedly draw samples from your data. This process simulates multiple independent training and test sets, providing a more stable and reliable evaluation of your model.

Resampling Strategies

Two of the most widely used resampling methods are:

• Cross validation: Creating non-overlapping subsets for training and testing

• Bootstrapping: Sampling with replacement, resulting in overlapping samples

The data

We will use the famous Iris dataset, which contains 150 samples from three species of the iris plant (iris setosa, iris virginica and iris versicolor). The data contains four features: the length and the width of the sepals and petals (in centimeters).

import seaborn as sns
import pandas as pd
from sklearn import datasets

# Get data
iris = datasets.load_iris(as_frame=True)
df = iris.frame
df['class'] = pd.Categorical.from_codes(iris.target, iris.target_names)

df.describe()

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	target
count	150.000000	150.000000	150.000000	150.000000	150.000000
mean	5.843333	3.057333	3.758000	1.199333	1.000000
std	0.828066	0.435866	1.765298	0.762238	0.819232
min	4.300000	2.000000	1.000000	0.100000	0.000000
25%	5.100000	2.800000	1.600000	0.300000	0.000000
50%	5.800000	3.000000	4.350000	1.300000	1.000000
75%	6.400000	3.300000	5.100000	1.800000	2.000000
max	7.900000	4.400000	6.900000	2.500000	2.000000

sns.scatterplot(data=df, x='sepal length (cm)', y='sepal width (cm)', hue="class");

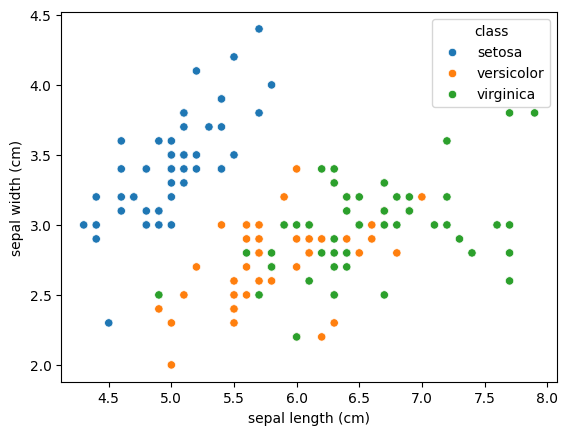
The goal of our model is to classify the flowering plants based on the two features shown in the plot (sepal length and width). Which of the following is true about the model and task at hand?

Validation Sets

Hyperparameters are parameters that are not learned from the data but set by the researcher before the training process.

The simplest form of cross validation is to simply split the dataset into two parts:

• Training set: Part of the data used for training

• Validation set: Part of the data used for testing (e.g. across different models and hyperparameters¹)

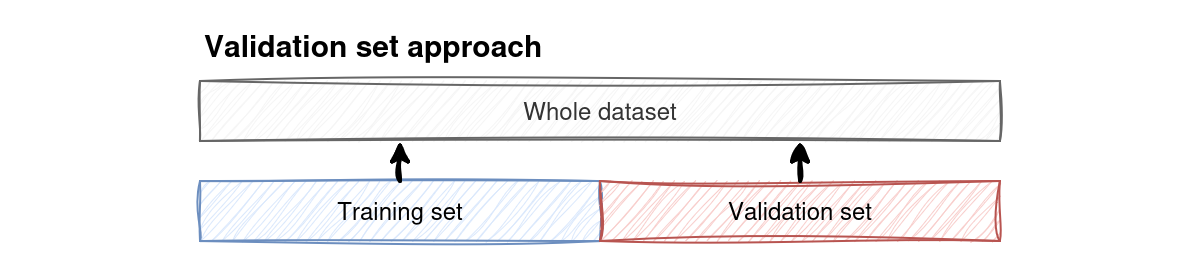
Fig. 3 The validation set splits the dataset into a training and a testing set (these do not necessarily need to be of equal size).

The training and testing set neither need to be of equal size nor do they need to be contiguous blocks in the data. Let’s try the validation set approach on the Iris data:

1. Define features and target data

iris = datasets.load_iris(as_frame=True)

# Features: sepal length and width; target: type of flower
X = df[["sepal length (cm)", "sepal width (cm)"]] 
y = df["target"]

2. Split the data into training and test samples

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=42)

3. Fit the model (we use a support vector classifier which you will learn about later in the seminar)

from sklearn import svm

model = svm.SVC(kernel='linear')
fit = model.fit(X_train, y_train)

4. Evaluate model performance

fit.score(X_test, y_test)

0.85

The score() method returns the accuray of our predictions. In this case, our algorithm correctly predicted the species of the flower in 85% of cases.

Hands on: In the editor below, we perform a classification for two splits in the the data. Please modify the code to first use 80% of the data for testing and 20% for training, and second to use 20% for training and 80% for testing. Before evaluating each model, think about what kind of results you would expect. Which model do you think will perform better?

Summary

The validation set approach is a quick and easy way to check how well a model performs. However, it has a major flaw: it puts all its trust in a single data split which can doom a great model or trick us into thinking a weak model performs better than it actually does.

Cross Validation (CV)

K-fold CV

To get more robust performance estimates, we need something smarter. Rather than worrying about if the split of data used for training and validation is biased, we will perform this splitting multiple times and use all of the splits in turn.

In k-fold CV we randomly dive the dataset into \(k\) equal-sized folds. In each fold, one sample is then designated as the validation set, while the remaining \(k-1\) samples are the training sets. The fitting process is repeated \(k\)-times, each time using a different fold as the validation set. At the end of the process, we can compute the average accuracy across all validation sets to obtain a more reliable estimate of the model’s overall performance.

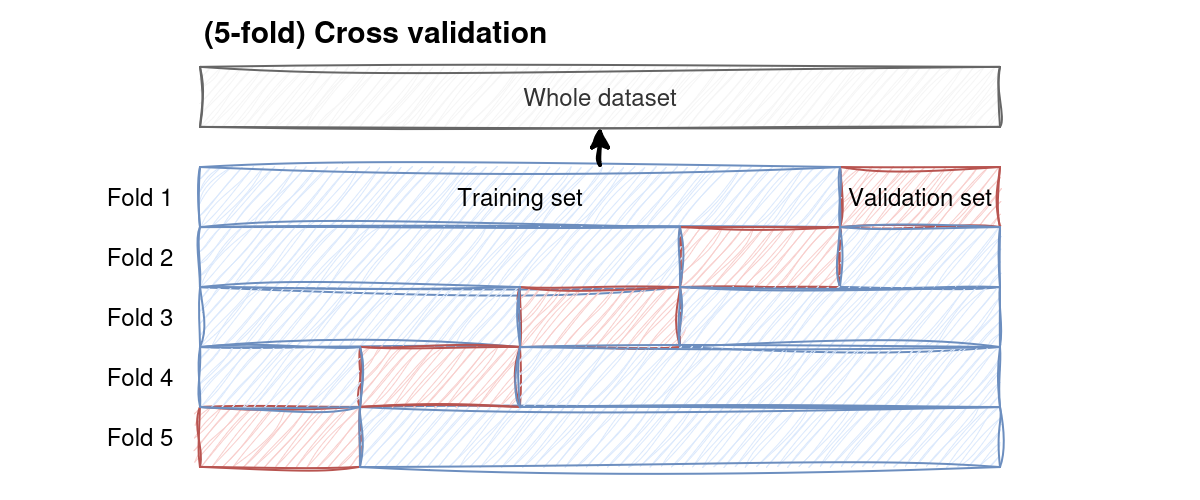
Fig. 4 K-fold cross validation splits the dataset into \(k\) equally sized parts and then trains the model on all possible combinations of it, keeping the proportion of train/test data constant.

Let`s try it on our data:

from sklearn.model_selection import KFold, cross_val_score

k_fold = KFold(n_splits = 5)
model = svm.SVC(kernel='linear')

scores = cross_val_score(model, X, y, cv=k_fold) 

print(f"Average accuracy:    {scores.mean()}")
print(f"Individual accuracies: {scores}")

Average accuracy:    0.6133333333333334
Individual accuracies: [1.         0.8        0.3        0.76666667 0.2       ]

If we are interested in the exact models, we can also run the training and evaluation explicitly which allows us to save the models:

from sklearn.base import clone

base_model = svm.SVC(kernel='linear')
score_list = []
model_list =  []

for train_index, test_index in k_fold.split(X):
    X_train, X_test = X.iloc[train_index], X.iloc[test_index] # iloc because X is a df
    y_train, y_test = y.iloc[train_index], y.iloc[test_index] # iloc because y is a df

    model = clone(base_model) # create a new copy of the model for every iteration
    model.fit(X_train, y_train)
    score = model.score(X_test, y_test)
    
    score_list.append(score)
    model_list.append(model)

print(f"Best performing model in split {score_list.index(max(score_list))}.")
print(f"Accuracy: {max(score_list)}")

Best performing model in split 0.
Accuracy: 1.0

Validatation set vs. k-fold

Comparing the two approaches, we see that the validation set approach shows a higher accuracy compared to CV. This tells us that our initial estimates were probably overly optimistic.

Try it yourself: Change the number of folds \(k\) and observe how the predicitions change. What do you feel like is a good tradeoff between bias and variance?

The choice of \(k\)

Choosing an appropriate k involves a tradeoff between bias, variance, and computational cost. A higher k generally provides a more stable and reliable estimate but comes with higher computational cost and also requires a sufficiently big dataset to still have a representative test set.

Generally speaking, \(k=5\) or \(k=10\) are common choices.

Leave-one-out CV (LOOCV)

LOOCV is a special case of k-fold cross validation, where \(k\) equals the number of observations. In LOOCV, the model is trained on all but one data point, and the remaining single observation is used for validation. This process repeats for each data point, ensuring every observation is used for testing exactly once.

While LOOCV provides a low-bias estimate, it is computationally expensive and may lead to high variance in model performance. The implementation is fairly similar, we just need to change the CV from KFold() to LeaveOneOut():

from sklearn.model_selection import LeaveOneOut

model = svm.SVC(kernel='linear')
loocv = LeaveOneOut()

scores = cross_val_score(model, X, y, cv = loocv)

print(f"Average accuracy:    {scores.mean()}")
print(f"Indidual accuracies: {scores}")

Average accuracy:    0.8
Indidual accuracies: [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1.
 1. 1. 0. 0. 0. 1. 0. 1. 0. 1. 0. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1.
 1. 1. 0. 0. 0. 0. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1.
 1. 1. 1. 1. 1. 0. 1. 0. 1. 1. 0. 1. 1. 1. 1. 0. 1. 0. 0. 1. 1. 1. 1. 0.
 1. 0. 1. 0. 1. 1. 0. 0. 1. 1. 1. 1. 1. 0. 0. 1. 1. 1. 0. 1. 1. 1. 0. 1.
 1. 1. 0. 1. 1. 0.]

Bootstrapping

Bootstrapping is a resampling method that helps us estimate how much a model’s results might vary if we collected a different dataset. The idea is simple: instead of having just one training set, we create many “new” datasets by sampling with replacement from the original data.

Each bootstrap sample is the same size as the original dataset, but because sampling is done with replacement, some observations will appear more than once, while others might not appear at all.

For each bootstrap iteration:

1. A new sample (the bootstrap sample) is drawn from the data.

2. The model is trained on this bootstrap sample.

3. The observations that were not included in that sample — called out-of-bag (OOB) samples — are used to test the model.

Repeating this process many times gives multiple estimates of model performance. The variability among these estimates provides insight into the model’s uncertainty and stability. In contrast, cross-validation divides the data into fixed folds and does not resample with replacement. Cross-validation is generally better for estimating predictive accuracy, while bootstrapping is often used to assess the uncertainty of model parameters or performance estimates.

We here outline the concept with 10 iterations:

import numpy as np
import pandas as pd
from sklearn import datasets, svm
from sklearn.utils import resample

# Load the data
iris = datasets.load_iris(as_frame=True)
df = iris.frame

n_iterations = 10
scores = []

for i in range(n_iterations):
    # Create a bootstrap sample
    bootstrap_sample = resample(df, replace=True, n_samples=len(df), random_state=i)
    
    # Determine the out-of-bag (OOB) samples: rows not in the bootstrap sample.
    oob_indices = df.index.difference(bootstrap_sample.index)
    
    # If no OOB samples are available, skip this iteration.
    if len(oob_indices) == 0:
        print(f"Iteration {i+1}: No out-of-bag samples, skipping iteration.")
        continue
    
    oob_sample = df.loc[oob_indices]
    
    # Define features and target for training and testing
    X_train = bootstrap_sample[["sepal length (cm)", "sepal width (cm)"]]
    y_train = bootstrap_sample["target"]
    X_test = oob_sample[["sepal length (cm)", "sepal width (cm)"]]
    y_test = oob_sample["target"]
    
    # Train and evaluate the model
    model = svm.SVC(kernel='linear')
    model.fit(X_train, y_train)
    
    score = model.score(X_test, y_test)
    scores.append(score)
    print(f"Iteration {i+1}: Accuracy = {score:.3f}")

print("\nMean Accuracy:", np.mean(scores))

Iteration 1: Accuracy = 0.774
Iteration 2: Accuracy = 0.825
Iteration 3: Accuracy = 0.759
Iteration 4: Accuracy = 0.817
Iteration 5: Accuracy = 0.818
Iteration 6: Accuracy = 0.778
Iteration 7: Accuracy = 0.827
Iteration 8: Accuracy = 0.729
Iteration 9: Accuracy = 0.807
Iteration 10: Accuracy = 0.839

Mean Accuracy: 0.7971433155841059

As you can see, the prediction accuracies are typically higher than those from cross-validation. This is expected because bootstrapping reuses parts of the same data across samples, leading to some overlap between training and evaluation data.