Model Selection

In neurocognitive psychology, we often collect huge amounts of data — sometimes thousands of measurements from different brain regions or many behavioral scores. Having more information can, in theory, help us make better predictions, but it also brings risks: too many variables can make analyses infeasible, lead to false discoveries, or cause models to learn noise instead of real effects.

The large p issue

Big data refers to large data sets with many predictors which often cannot be processed or analyzed using traditional data processing techniques. For our prediction models, this brings some issues:

• While the linear model can in theory still be used for such data, the ordinary least squares fit becomes infeasible, especially when p > n

• The large amount of features reduce interpretability

This is where linear model selection becomes essential, offering techniques to refine our models and extract meaningful insights from high-dimensional data.

Today’s data: Hitters

For practical demonstration, we will use the Hitters dataset. This dataset provides Major League Baseball Data from the 1986 and 1987 seasons. It contains 322 observations of major league players on 20 variables (so it’s not big data, but we can pretend it is). The Research aim is to predict a baseball player’s salary on the basis of various predictors associated with the performance in the previous year. You can check its contents here: https://islp.readthedocs.io/en/latest/datasets/Hitters.html

import statsmodels.api as sm 

# Get the data
hitters = sm.datasets.get_rdataset("Hitters", "ISLR").data

For computational reasons, we will not include all predictors but only a smaller subset:

# Keep a total of 10 variables - the target ´Salary´ and 9  features.
hitters_subset = hitters[["Salary", "CHits", "CAtBat", "CRuns", "CWalks", "Assists", "Hits", "HmRun", "Years", "Errors"]].copy()

# Remove rows with missing vlaues
hitters_subset.dropna(inplace=True)

hitters_subset.head()

	Salary	CHits	CAtBat	CRuns	CWalks	Assists	Hits	HmRun	Years	Errors
rownames
-Alan Ashby	475.0	835	3449	321	375	43	81	7	14	10
-Alvin Davis	480.0	457	1624	224	263	82	130	18	3	14
-Andre Dawson	500.0	1575	5628	828	354	11	141	20	11	3
-Andres Galarraga	91.5	101	396	48	33	40	87	10	2	4
-Alfredo Griffin	750.0	1133	4408	501	194	421	169	4	11	25

Let’s also take a look at the correlation matrix to check for potential multicollinearity, which can affect the stability of linear regression models.

import seaborn as sns

sns.heatmap(hitters_subset.corr(), annot=True, cmap="coolwarm", fmt=".2f");

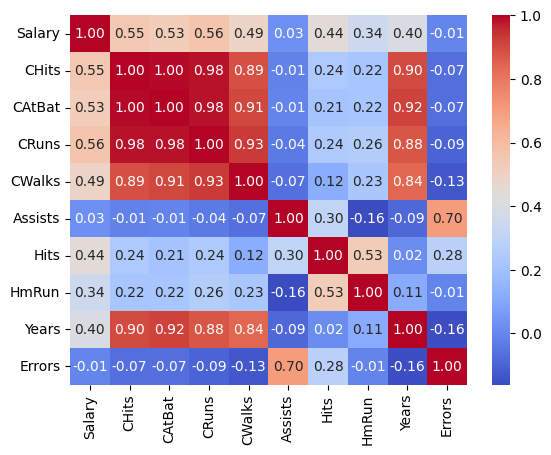
The heatmap reveals strong correlations between several predictors:

• CHits and CAtBat show a correlation of 1,

• CHits and CRuns have a very strong correlation of 0.98,

We thus remove two of the correlated features:

features_drop = ["CRuns", "CAtBat"]
hitters_subset = hitters_subset.drop(columns=features_drop)

Handling big data in linear models

Handling big data

To handle large datasets efficiently in linear modeling, we will introduce three methods:

• Subset Selection

• Dimensionality Reduction

• Regularization / Shrinkage

Subset Selection

In subset selection we identify a subset of p predictos that are truly related to the outcome. The model get fitted using least squares on the reduces set of variables.

How do we determine which variables are relevant?!

Best Subset Selection

We will start with performing Best Subset Selection (also called exhaustive search) as implemented in the mlxtend package. It has great documentation, e.g. for the exhaustive search. In short, this approach is a brute-force evaluation of feature subsets. A specific performance metric (e.g. MSE, R², or accuracy) is optimized given an arbitrary regressor or classifier. For example, if we have 4 features, the algorithm will evaluate all 15 possible combinations of features.

Before we start the subset selection, we first define the target and the features:

import numpy as np

y = hitters_subset["Salary"]
X = hitters_subset.drop("Salary", axis=1)

We first split our data into training and test dataset. Although the selection function uses cross-validation to identify the best subset of predictors (Step 3), this evaluation is done during the selection process and can still overfit to the data. To fairly assess how the final model performs on new data, we split off a test set and use it only after feature selection is complete.

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

Purpose	What is it for?	When?
Cross Validation in selection function	Helps choose the best subset of features	During selection
Test Set Evaluation	Checks how well the final model performs	After selection

We then run Best Subset Selection on the training data:

from sklearn.linear_model import LinearRegression
from mlxtend.feature_selection import ExhaustiveFeatureSelector

efs = ExhaustiveFeatureSelector(
        estimator=LinearRegression(),
        min_features=1,
        max_features=X_train.shape[1],
        scoring='r2',
        cv=5,
        print_progress=False)

efs.fit(X_train, y_train)

print('Best R²: %.2f' % efs.best_score_)
print('Best subset (indices):', efs.best_idx_)
print('Best subset (corresponding names):', efs.best_feature_names_)

Best R²: 0.41
Best subset (indices): (1, 3, 4)
Best subset (corresponding names): ('CWalks', 'Hits', 'HmRun')

If you are interested in the details, they are stored in the metric dictionary:

import pandas as pd

df = pd.DataFrame.from_dict(efs.get_metric_dict()).T
df.sort_values('avg_score', inplace=True, ascending=False)
df

	feature_idx	cv_scores	avg_score	feature_names	ci_bound	std_dev	std_err
47	(1, 3, 4)	[0.38067374180608526, 0.463839312906159, 0.505...	0.412539	(CWalks, Hits, HmRun)	0.100218	0.077973	0.038987
90	(1, 3, 4, 6)	[0.3878486031208028, 0.4634739461791568, 0.493...	0.408445	(CWalks, Hits, HmRun, Errors)	0.094497	0.073522	0.036761
83	(1, 2, 3, 4)	[0.3813017586747449, 0.4658246874129488, 0.506...	0.404694	(CWalks, Assists, Hits, HmRun)	0.098463	0.076607	0.038304
89	(1, 3, 4, 5)	[0.33058568684405754, 0.46099452778892, 0.5147...	0.403253	(CWalks, Hits, HmRun, Years)	0.105549	0.082121	0.041061
114	(1, 2, 3, 4, 6)	[0.3751200780670817, 0.4651398463048052, 0.496...	0.401198	(CWalks, Assists, Hits, HmRun, Errors)	0.095867	0.074588	0.037294
...	...	...	...	...	...	...	...
58	(2, 5, 6)	[0.14956857373046695, 0.13751233647954653, 0.1...	0.122419	(Assists, Years, Errors)	0.120381	0.093661	0.04683
5	(5,)	[0.14935846878458914, 0.1343083510706763, 0.12...	0.122124	(Years,)	0.135551	0.105464	0.052732
2	(2,)	[-0.0025851222923383155, -0.007245558244625583...	-0.040331	(Assists,)	0.04707	0.036622	0.018311
6	(6,)	[-0.02226936534097579, -0.006949819455392525, ...	-0.051379	(Errors,)	0.045878	0.035695	0.017847
21	(2, 6)	[-0.04083051774641855, -0.007183353236134726, ...	-0.057133	(Assists, Errors)	0.042413	0.032998	0.016499

127 rows × 7 columns

Forward Stepwise Selection

Forward Stepwise Selection is a greedy feature‐selection method that starts with no features and, at each step, adds the single feature whose inclusion most improves the model’s performance. This “add the best remaining feature” is repeated until a desired number of features is reached, at which point the algorithm stops and returns the best subset.

An important parameter is k_features, which determines the number of features to select. We can, pass an integer (must be less than the total number of available features), a tuple (the algorithm will then evaluate all subset sizes between the min and max value), or one of two string options ("best", or "parsimonious"). Please refer to the documentation for further details.

from mlxtend.feature_selection import SequentialFeatureSelector

sfs_forward = SequentialFeatureSelector(
    estimator=LinearRegression(),
    k_features=(1, X_train.shape[1]),
    forward=True,
    scoring='r2',
    cv=5,
    verbose=0)
    
sfs_forward.fit(X_train, y_train)

print(f">> Forward SFS:")
print(f"   Best CV R²      : {sfs_forward.k_score_:.3f}")
print(f"   Optimal # feats : {len(sfs_forward.k_feature_idx_)}")
print(f"   Feature indices : {sfs_forward.k_feature_idx_}")
print(f"   Feature names   : {sfs_forward.k_feature_names_}")

>> Forward SFS:
   Best CV R²      : 0.413
   Optimal # feats : 3
   Feature indices : (1, 3, 4)
   Feature names   : ('CWalks', 'Hits', 'HmRun')

You can see we ended up with the same three predictors as in best subset selection: CWalks, Hits, HmRun. However, this is not necessarily always the case — best subset and stepwise selection can, and often do, lead to different results. In our case we only had a small number of predictors, which makes it more likely to end up with the same subset.

Backward Stepwise Selection

Backward Stepwise Selection begins with the full feature set and, at each step, removes the single feature whose exclusion most improves (or least harms) model performance. We keep repeating this “remove the worst feature” step until only the desired number of features remains, and then the algorithm returns that reduced subset:

sfs_backward = SequentialFeatureSelector(
    estimator=LinearRegression(),
    k_features=(1, X_train.shape[1]),
    forward=False,
    floating=False,
    scoring='r2',
    cv=5,
    verbose=0)

sfs_backward.fit(X_train, y_train)

print(f"<< Backward SFS:")
print(f"   Best CV R²      : {sfs_backward.k_score_:.3f}")
print(f"   Optimal # feats : {len(sfs_backward.k_feature_idx_)}")
print(f"   Feature indices : {sfs_backward.k_feature_idx_}")
print(f"   Feature names   : {sfs_backward.k_feature_names_}")

<< Backward SFS:
   Best CV R²      : 0.413
   Optimal # feats : 3
   Feature indices : (1, 3, 4)
   Feature names   : ('CWalks', 'Hits', 'HmRun')

Subset Selection Summary

Best Subset Selection	Forward Stepwise Selection	Backward Stepwise Selection
+ will find the best model	- not guaranteed to find best model	- not guaranteed to find best model
- may overfit with large p	+ possible to use when p is very large	+ possible to use when p is very large, given p<n
- computationally very expensive	+ computationally less demanding	+ computationally less demanding

What next?

Once we have identified the features that are relevant for predicting the outcome, let`s evaluate the model performance and estimate true test error with the thee predictors identified by Best Subset Selection and Forward Stepwise Seletion.

import numpy as np
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.linear_model import LinearRegression

selected_features = list(sfs_backward.k_feature_names_)

# Subset the data
X_train_subset = X_train[selected_features]
X_test_subset = X_test[selected_features]

# Fit the model
model = LinearRegression()
model.fit(X_train_subset, y_train)

# Get predictions anf performance
y_pred = model.predict(X_test_subset)

mse_test = mean_squared_error(y_test, y_pred)
rmse_test = np.sqrt(mse_test)
r2_test = r2_score(y_test, y_pred)

print(f"Test MSE:  {mse_test:.2f}")
print(f"Test RMSE: {rmse_test:.2f}")
print(f"Test R²:   {r2_test:.4f}")

Test MSE:  182321.00
Test RMSE: 426.99
Test R²:   0.2492

So in sum:

• On average, our predictions deviate from the actual salary by about 426 thousand dollars.

• Our model explains ~25% of the variance in salary.

Regularization and Dimensionality Reduction

As mentioned before, regularization and dimensionality reduction are two other measures of dealing with large numbers of predictors. Regularization techniques will be introduced in the next session, and dimensionality reduction will be introduced in the Principal Component Analysis session.