Generalized Additive Models#
Generalized Additive Models (GAMs) offer a powerful and flexible extension to traditional linear models by allowing for non-linear, additive relationships between each predictor and the outcome. Unlike standard linear regression, which assumes a strictly linear association between predictors and the response variable, GAMs replace each linear term with a smooth function, enabling the model to better capture complex patterns in the data. Thanks to their additive structure, each predictor contributes independently to the model, making it easy to interpret the effect of each variable.
So instead of using the standard linear function
we have something like this:
In short, instead of using fixed slope coefficients \(b_i\) that assume a straight-line relationship, we replace them with flexible (possibly non-linear) smooth functions \(f_i\) for each predictor. These functions can be anything from constant functions and polynomials to wavelets.
So in comparison to simple splines regression which (last semester) was introduced to predict \(y\) on the basis of a single predictor \(x\), GAMs are a generalization which allows us to predict \(y\) given multiple predictors \(x_1 ... x_p\).
Today’s data: The Diabetes dataset#
For today’s practical demonstration, we will work with the Diabetes dataset from scikit-learn. This dataset contains medical information collected from 442 diabetes patients, including:
Features: 10 baseline measures from the beginning of the study: age, sex, Body Mass Index (BMI), average blood pressure, as well as six blood serum measurements (e.g. cholesterol, blood sugar, etc.)
Target: A quantitative measure of disease progression one year after the baseline measurements were taken.
You can find more information here.
from sklearn import datasets
from sklearn.model_selection import train_test_split
# Get data
diabetes = datasets.load_diabetes(as_frame=True)
X = diabetes.data
y = diabetes.target
# Split the data into training and test set
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
To explore the relationships between each feature and the target, we plot each predictor against the disease progression outcome. These scatter plots with simple linear regressions help us to visually assess whether the relationship between a feature and the target is linear or if we need a more flexible model approach:
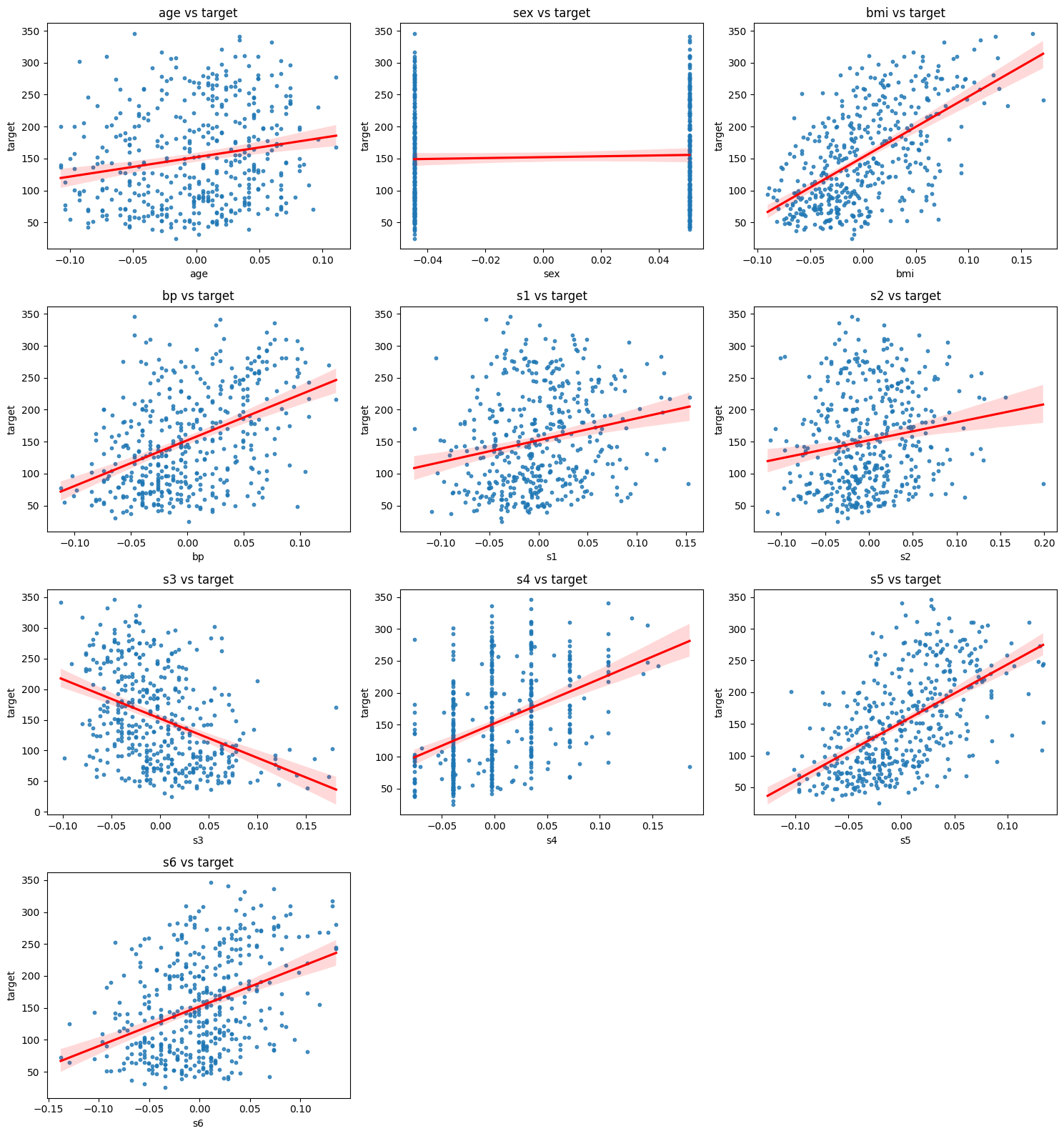
Although the linear regression fits seem to be reasonable, we might suspect that a more flexible approach could be beneficial, so let’s try it!
GAMs in Python#
There are multiple options for implementing GAMs. We will here use statsmodels, as you should already be familiar with it from the previouis semester. The workflow is the following:
Separate smooth (continuous) and categorical features
Create spline basis functions for the continuous features using B-splines
Fit the GAM with both the smooth and categorical predictors
from statsmodels.gam.api import GLMGam, BSplines
spline_features = ['age', 'bmi', 'bp', 's1', 's2', 's3', 's4', 's5', 's6']
categorical_features = ['sex']
# Create smoother for continuous variables
bs = BSplines(X_train[spline_features], df=[6]*len(spline_features), degree=[3]*len(spline_features))
# Fit GAM with smoother and exog for categorical
gam = GLMGam(y_train, exog=X_train[categorical_features], smoother=bs)
res = gam.fit()
print(res.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: target No. Observations: 309
Model: GLMGam Df Residuals: 263.00
Model Family: Gaussian Df Model: 45.00
Link Function: Identity Scale: 2998.6
Method: PIRLS Log-Likelihood: -1650.5
Date: Mon, 27 Oct 2025 Deviance: 7.8864e+05
Time: 13:07:03 Pearson chi2: 7.89e+05
No. Iterations: 3 Pseudo R-squ. (CS): 0.7023
Covariance Type: nonrobust
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
sex -289.6664 78.808 -3.676 0.000 -444.126 -135.206
age_s0 -32.4246 50.442 -0.643 0.520 -131.289 66.439
age_s1 -61.4878 28.887 -2.129 0.033 -118.105 -4.871
age_s2 -5.3132 39.461 -0.135 0.893 -82.655 72.029
age_s3 -42.6463 38.246 -1.115 0.265 -117.608 32.315
age_s4 18.0807 60.041 0.301 0.763 -99.598 135.759
bmi_s0 43.8396 54.386 0.806 0.420 -62.756 150.435
bmi_s1 19.4553 33.130 0.587 0.557 -45.479 84.390
bmi_s2 97.0613 48.512 2.001 0.045 1.980 192.142
bmi_s3 57.8888 49.412 1.172 0.241 -38.956 154.734
bmi_s4 252.4823 59.944 4.212 0.000 134.995 369.969
bp_s0 30.6097 58.249 0.525 0.599 -83.556 144.775
bp_s1 38.3179 38.098 1.006 0.315 -36.353 112.989
bp_s2 76.9274 49.565 1.552 0.121 -20.218 174.073
bp_s3 81.3546 48.055 1.693 0.090 -12.832 175.542
bp_s4 147.7945 57.513 2.570 0.010 35.070 260.519
s1_s0 58.6364 106.319 0.552 0.581 -149.744 267.017
s1_s1 -125.9137 154.677 -0.814 0.416 -429.075 177.247
s1_s2 -233.7171 336.444 -0.695 0.487 -893.135 425.701
s1_s3 -439.3612 450.331 -0.976 0.329 -1321.994 443.272
s1_s4 -351.3655 556.288 -0.632 0.528 -1441.670 738.939
s2_s0 26.6938 99.713 0.268 0.789 -168.741 222.128
s2_s1 125.9591 143.712 0.876 0.381 -155.712 407.630
s2_s2 274.4660 332.759 0.825 0.409 -377.729 926.661
s2_s3 464.5552 472.107 0.984 0.325 -460.758 1389.868
s2_s4 262.7111 613.544 0.428 0.669 -939.813 1465.235
s3_s0 14.3698 64.625 0.222 0.824 -112.292 141.032
s3_s1 40.7103 49.233 0.827 0.408 -55.784 137.205
s3_s2 39.5808 95.906 0.413 0.680 -148.392 227.554
s3_s3 101.7901 148.474 0.686 0.493 -189.214 392.794
s3_s4 120.5364 187.063 0.644 0.519 -246.101 487.174
s4_s0 -37.5731 46.372 -0.810 0.418 -128.461 53.315
s4_s1 11.2719 36.681 0.307 0.759 -60.622 83.166
s4_s2 -64.0818 65.922 -0.972 0.331 -193.286 65.123
s4_s3 48.0156 87.235 0.550 0.582 -122.961 218.992
s4_s4 25.2745 109.679 0.230 0.818 -189.693 240.242
s5_s0 -22.0863 49.386 -0.447 0.655 -118.882 74.709
s5_s1 26.4723 30.680 0.863 0.388 -33.660 86.605
s5_s2 127.4137 69.308 1.838 0.066 -8.428 263.255
s5_s3 174.7068 139.025 1.257 0.209 -97.776 447.190
s5_s4 264.2489 238.234 1.109 0.267 -202.681 731.179
s6_s0 -72.3705 79.891 -0.906 0.365 -228.954 84.213
s6_s1 -33.7499 51.643 -0.654 0.513 -134.969 67.469
s6_s2 -74.4075 61.859 -1.203 0.229 -195.648 46.833
s6_s3 -6.0775 59.770 -0.102 0.919 -123.224 111.069
s6_s4 -28.6995 62.161 -0.462 0.644 -150.532 93.133
==============================================================================
For the B-splines1 we choose:
df=[6]*len(spline_features)-> 6 basis functions per featuredegree=[3]*len(spline_features)-> cubic splines (degree 3)
The output includes parameter estimates for all spline basis functions and categorical variables:
The
coefcolumn shows the estimated effect.The
P>|z|column tells you whether the estimate is statistically significantThe Pseudo
R-squared (CS)gives a rough measure of model fit (here around 0.70)
Due to the additive nature of GAMs, we can isolate and visualise the effect of each smooth term individually. This helps us understand the relationship between each predictor and the response, controlling for all other variables:
import matplotlib.pyplot as plt
fig, ax = plt.subplots(3,3, figsize=(7,7))
for i, feature in enumerate(spline_features):
res.plot_partial(i, cpr=True, ax=ax[i//3, i%3])
ax[i//3, i%3].set_title(f"Partial Effect: {feature}")
plt.tight_layout()
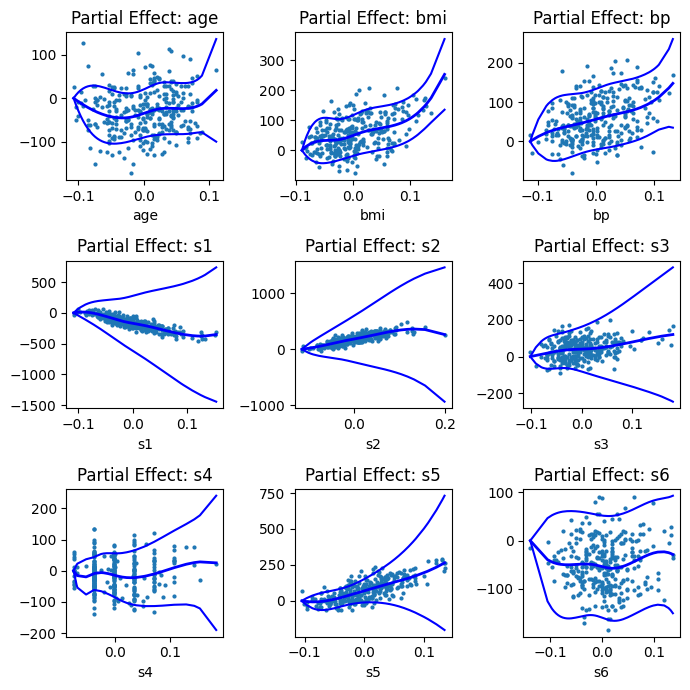
Each subplot shows how the modelled relationship between a feature and the target behaves nonlinearly. The cpr=True option adds confidence intervals around the estimated smooth curve.
Summary
GAMs allow flexible, interpretable models where you don’t assume linearity for every predictor.
statsmodelsmakes it easy to combine smooth terms (B-splines or alternatively Cyclic Cubic Splines) with categorical or linear predictors.You can inspect smooth effects with
.plot_partial(), and linear terms directly from the model summary.

