5.4 Exercises

# Required imports for the exercises
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt

Exercise 1: Creating and exploring numpy arrays

1. Array initialization

• Create a one-dimensional NumPy array of integers from 0 to 9 using np.arange()

• Print the array and its shape

2. Array conversion

• Convert the Python list [10, 20, 30, 40, 50] to a NumPy array by using np.asarray()

• Print the resulting array as well as its type

3. Reshaping an array

• Use np.reshape() to transform the array from the first step into a two-dimensional 2x5 array

• Print the reshaped array and verify its new shape

4. Arrays and lists

• Have a look at the documentation and create a three dimensional array of shape (2,2,2) which is filled with zeros

• How would such a shape look in the real world? Print the array on the screen. Make sure you understand how the values displayed visually map onto the dimensions of the array

• Voluntary exercise: Can you generate such a 3D array with only the np.array() method? Hint: A three-diensional array can be seen as a list of lists of lists.

# Exercise 1

Exercise 2: Generating arrays and basic calculations

1. Random arrays

• Look up the documentation of np.random.randint() and create a 3x4 array with random integers between 1 and 100

• Calculate and print the sum of all the elements

2. Arithmetic operations

• Create an array from the values [5, 10, 15, 20]

• Add 5 to each element of the array

• Multiply the entire array by 2 and print the result

3. Array statistics

• Create a 1D array with values ranging from 0 to 10 using np.linspace() with 21 evenly spaced data points

• Compute and print the mean, median, and standard deviation of the array using NumPy functions

# Exercise 2

Exercise 3: Indexing and slicing arrays

1. Basic indexing

• Create a 4x4 array of random integers between 10 and 50 using np.random.randint()

• Access and print the element in the second row and third column

2. Slicing an array

• Slice and print the first two rows and the last two columns of the array from the previous step

3. Conditional indexing

• Create a 1D array of 10 random integers between 0 and 100

• Extract all values greater than 50 and store them in a new array

• Print the original array and the extracted values

# Exercise 3

Exercise 4: Pandas DataFrames

1. Please create a Pandas DataFrame with columns “Name”, “Age”, and “City” for 5 people and print out the first two rows.

2. Filter out all rows where the “Age” column is greater than 30, and calculate the average age for the remaining rows.

# Exercise 4

Exercise 5: More DataFrames

1. Load the Yeatman data from https://yeatmanlab.github.io/AFQBrowser-demo/data/subjects.csv into a DataFrame.

2. Print the head of the DataFrame to get an overview of what is in there.

3. Add a filter column for people younger than 30 and call it'Age < 30'.

4. Calculate the average age and IQ for people younger than 30 as well as for the older people and compare the results.

Hints:

• The conditions are mutually exclusive (i.e., a person is either younger than 30 or not), meaning you only need a single filter column to cover both conditions.

• You can simply use the tilde operator (~) for indexing, which in pandas means “not”. Indexing people 30 and older thus looks like this: df[~df['Age < 30']].

# Exercise 5

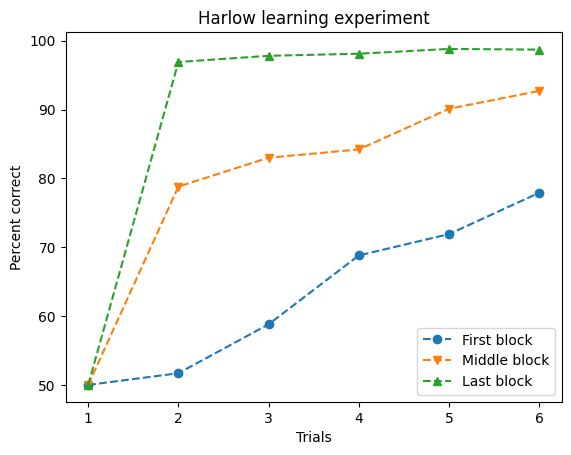
Exercise 6: Plotting with matplotlib

The plot method has multiple other keyword arguments to control the appearance of its results. For example, the color keyword argument controls the color of the lines. One way to specify the color of each line is by using a string that is one of the named colors specified in the Matplotlib documentation. Use this keyword argument to change the color of the lines in the plot.

trials = [1, 2, 3, 4, 5, 6]
first_block = [50, 51.7, 58.8, 68.8, 71.9, 77.9]
middle_block = [50, 78.8, 83, 84.2, 90.1, 92.7]
last_block = [50, 96.9, 97.8, 98.1, 98.8, 98.7]

fig, ax = plt.subplots()

ax.plot(trials, first_block, marker='o', linestyle='--', label="First block")
ax.plot(trials, middle_block, marker='v', linestyle='--', label="Middle block")
ax.plot(trials, last_block, marker='^', linestyle='--', label="Last block")

ax.legend()
ax.set(xlabel='Trials', ylabel='Percent correct', title='Harlow learning experiment')

plt.show()

Exercise 7: Reaction time plotting

Please create a bar plot for the results of a reaction time experiment. The figure should contain:

• A single plot with three bars (one for each condition)

• Colors: skyblue for no distraction, orange for low distraction, and red for high distraction

• A title, an x-axis label, and an y-axis label

conditions = ['No Distraction', 'Low Distraction', 'High Distraction']
reaction_times = [250, 300, 400]

Exercise 8: EEG signal processing

Please create a single figure, which contains three subplots containing artificial EEG signal. The subplots should be stacked below each other. All plots should contain labels and a legend.

1. EEG signal plotting:

• Plot the artificial EEG signal using matplotlib.

2. Noise addition:

• Add Gaussian noise (mean = 0, std = 0.5) to the EEG signal. Hint: You can use np.random.normal() to add the noise.

• Plot the noisy EEG signal and compare it with the original signal.

3. Filtering:

• Apply a simple threshold filter to remove values outside the range [-1, 1]. Hint: You can use np.clip() for this.

• Plot the filtered signal.

# Parameters
sampling_rate = 250  # Sampling rate in Hz
time = np.linspace(0, 1, 250)  # Time vector 1 seconds duration, 250 samples (x-values of the plot) 
frequency = 10  # "Alpha wave" frequency in Hz

# Generating the sine wave signal
eeg_signal = np.sin(2 * np.pi * frequency * time)

Exercise 9: Plotting an image

The following example downloads fMRI data from the internet and averages it over time, so you arrive at a single 3D image of the brain with shape (61, 73, 61). As images are usually 2-dimensional, we can visualize it by plotting the three aex separately.

1. Create three subplots.

2. Plot the brain in its three different planes (horizontal, coronal, saggital) by using matplotlib’s imshow() function.

Hint: You can index the middle of the brain in each axis with e.g. averaged_fmri[averaged_fmri.shape[0] // 2, :, :] (// is a floor division operator which returns the largest integer less or equal than the result of the divison).

Important: If you use Google colab, you need to install the nilearn and nibabel packages by typing !pip install nilearn nibabel in a code cell before importing them.

from nilearn import datasets
import nibabel as nib

haxby_dataset = datasets.fetch_adhd(n_subjects=1) # Download the Haxby dataset
fmri_img = nib.load(haxby_dataset.func[0]) # Load the fMRI data using nibabel
fmri_data = fmri_img.get_fdata() # Convert to a 4D numpy array
print(f"Shape of the fMRI data: {fmri_data.shape}")
averaged_fmri = np.mean(fmri_data, axis=3) # Average over the time dimension to get a single image
print(f"Shape of the fMRI data (averaged over time): {averaged_fmri.shape}")

Shape of the fMRI data: (61, 73, 61, 176)
Shape of the fMRI data (averaged over time): (61, 73, 61)

Voluntary Exercise 1: More NumPy indexing

1. Generate a random 10x10 matrix with values between 10 and 99

2. Find the index of the largest value by using np.where() and replace it with 0

3. Find the row-wise and column-wise sums of the updated array and print the result.

# Voluntary exercise 1

Voluntary exercise 2: More Pandas operations and plotting

Given the DataFrame with columns “Product”, “Sales”, and “Date”:

1. Create a new column called Cumulative_Sale showing the cumulative sales by product over time

2. Plot a line graph of cumulative sales for each product.

Hints:

• DataFrames have a .cumsum() method which you can use

• You can loop over the unique products like so: for product in df['Product'].unique():

df = pd.DataFrame({
    'Product': ['A', 'A', 'B', 'B', 'A', 'B'],
    'Sales': [100, 150, 200, 50, 300, 400],
    'Date': pd.date_range(start='2023-01-01', periods=6, freq='D')
})

Voluntary exercise 3: Large plotting layouts

1. Create a 3x3 grid of subplots

2. For each subplot, plot a different function (e.g., sin(x), cos(x), tan(x), etc.)

3. Customize the titles, axes, and tick labels of each subplot.

Hints:

• Try to do the plotting in a single loop. The potential loop could look like this: for ax, func in zip(axes.flat, functions):, with axes being the axex object from plt.subplots and functions being a list containing the relevant functions

• You can find a list of usable mathematical functions here

• The name of the mathematical function can be accessed through the func.__name_ attribute

# Voluntary exercise 3

Voluntary exercise 4: Bar plot with seaborn

Recall Exercise 7, which involved the plotting of a bar plot. The data is now extended to contain multiple measurements, which should be represented in the figure through errorbars.

1. Convert the data into a DataFrame and use this as input for the plotting function.

2. Create a barplot using sns.barplot(). The plot should contain errorbars showing the standard deviation, a pastel color palette, labels, and a title.

import seaborn as sns 

conditions = ['No Distraction', 'Low Distraction', 'High Distraction']
reaction_times = [
    [240, 250, 260, 255],  # No Distraction
    [290, 300, 310, 295],  # Low Distraction
    [390, 400, 410, 405]   # High Distraction
]

Voluntary exercise 5: Visualizing penguin flipper lengths across species and islands

The Palmer Penguins dataset provides measurements for three penguin species: Adelie, Chinstrap, and Gentoo, across three islands. The dataset includes information about bill length, bill depth, flipper length, and body mass. In this exercise, you’ll create a violin plot to visualize the distributions of a chosen feature (e.g., flipper length) across species and islands.

1. Load the Palmer Penguins dataset from Seaborn. Remove rows with missing values.

2. Use Seaborn’s whitegrid theme

3. Create a violin plot to represent the distribution of flipper lengths for each penguin species. Use a neutral color (lightgray) for the violin plot background and remove internal lines.

4. Use a strip plot to overlay individual data points for each species. Color the points based on the island (island column). Spread the points with jitter to reduce overlap and improve visibility.

5. ustomize the points: Increase size for better visibility, add a black edge color and set a small edge width, and make the points semi-transparent (alpha=0.8) to handle overlapping.

6. Add a descriptive title. Label the x-axis as “Penguin Species” and the y-axis as “Flipper Length (mm)”.

7. Adjust the legend to make it clear which colors correspond to which islands. Place the legend in the upper left corner of the plot.

8. Ensure the figure size is appropriate (10x6 inches). Display the final plot.

9. Answer the following questions: On which island to penguins have the longest flipper length? Which penguins inhabitate which island?

# Voluntary exercise 5