13.2 Regression Splines

13.2 Regression Splines#

To fit regression splines, we continue with the same data as in the previous section. Again, we want to predict wage from age in the Mid-Atlantic Wage Dataset.

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import patsy
import statsmodels.api as sm
from ISLP import load_data

# Load the data
df = load_data('Wage')

Fitting piecewise linear splines#

Similar to fitting a stepwise function, we first need to create the design matrix for our transformed predictor age. This time we specify two knots (at age 40 and 60), and first-order polynomial:

transformed_age = patsy.dmatrix("bs(age, knots=(40,60), degree=1)",
                                data={"age": df['age']},
                                return_type='dataframe')

We then create and fit the model:

# Fit the model
model = sm.OLS(df['wage'], transformed_age)
model_fit = model.fit()

print(model_fit.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                   wage   R-squared:                       0.083
Model:                            OLS   Adj. R-squared:                  0.083
Method:                 Least Squares   F-statistic:                     90.93
Date:                Wed, 09 Apr 2025   Prob (F-statistic):           2.59e-56
Time:                        08:53:32   Log-Likelihood:                -15319.
No. Observations:                3000   AIC:                         3.065e+04
Df Residuals:                    2996   BIC:                         3.067e+04
Df Model:                           3                                         
Covariance Type:            nonrobust                                         
========================================================================================================
                                           coef    std err          t      P>|t|      [0.025      0.975]
--------------------------------------------------------------------------------------------------------
Intercept                               71.6381      2.638     27.152      0.000      66.465      76.811
bs(age, knots=(40, 60), degree=1)[0]    49.8144      3.429     14.529      0.000      43.092      56.537
bs(age, knots=(40, 60), degree=1)[1]    45.8718      3.024     15.169      0.000      39.942      51.801
bs(age, knots=(40, 60), degree=1)[2]    17.2156      9.277      1.856      0.064      -0.975      35.406
==============================================================================
Omnibus:                     1083.113   Durbin-Watson:                   1.963
Prob(Omnibus):                  0.000   Jarque-Bera (JB):             4829.501
Skew:                           1.702   Prob(JB):                         0.00
Kurtosis:                       8.201   Cond. No.                         15.2
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

The coeff column indicates the coefficients of wage regressing on each basis function of age, i.e. \(b_0, b_1, b_2, b_3\).

However, spline regression coefficients are not analogous to slope coefficients in simple linear regression and they are not directly interpretable as increase or decrease on \(Y\) given one-unit increase on \(X\)! Spline regression coefficients scale the computed basis functions for a given value of \(X\) (see slides from the multivariate statistics lecture).

We can nevertheless calculate the slopes of the fitted spline starting from our coefficients:

\[ \text{slope}_1 = \frac{\text{coef}[1]}{\text{knot}[0] - \text{knot.boundary.left}} = \frac{\text{49.81}}{\text{40 - 18}} = 2.26 \]
\[ \text{slope}_2 = \frac{\text{coef}[2] - \text{coef}[1]}{\text{knot}[1] - \text{knot}[0]} = \frac{\text{45.71 - 49.81}}{\text{60 - 40}} = -0.2 \]
\[ \text{slope}_3 = \frac{\text{coef}[3] - \text{coef}[2]}{\text{knot.boundary.right} - \text{knot}[1]} = \frac{\text{17.21 - 45.71}}{\text{80 - 60}} = -1.42 \]

Plotting the model#

# Create evenly spaced values to plot the model predictions
xp = np.linspace(df['age'].min(), df['age'].max(), 100)
xp_trans = patsy.dmatrix("bs(xp, knots=(40,60), degree=1)",
                         data={"xp": xp},
                         return_type='dataframe')

# Use model fitted before to predict wages for generated age values
predictions = model_fit.predict(xp_trans)

# Plot the original data and the model fit
fig, ax = plt.subplots(figsize=(8,5))                           # Create figure object

sns.scatterplot(data=df, x="age", y="wage", alpha=0.4, ax=ax)   # Plot observations
ax.axvline(40, linestyle='--', alpha=0.4, color="black")        # Cut point 1
ax.axvline(60, linestyle='--', alpha=0.4, color="black")        # Cut point 2
ax.plot(xp, predictions, color='red')                           # Draw prediction
ax.set_title("Linear (first-order) spline regression");
../../../_images/30637e0e73b05aef92c1f7d2f61963b42b7480296705604f35e9cc64aeef655a.png

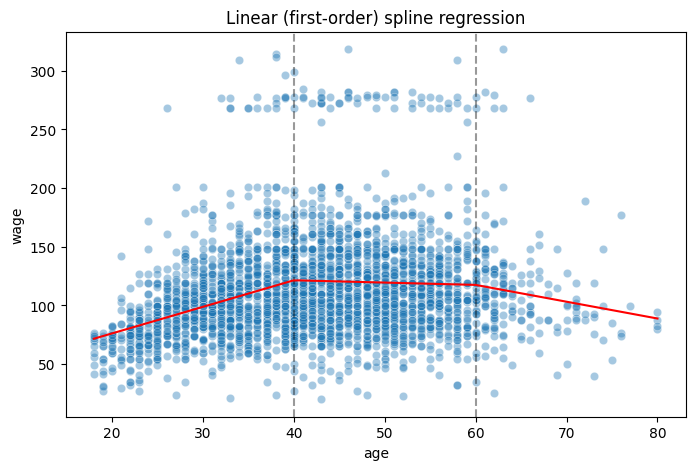
The model plot shows that we have gone from fitting an intercept (i.e., a horizontal line) in each bin to fitting a linear function in each bin.

Contents