GLM#
Data preparation#
We will use the diabetes data set from the sklearn library for the following three exercises.
Loading the data
The code for loading the dataset is already provided. Look at the documentation of the
load_diabetes()function to familiarize yourself with the function and its outputs.Use the
DESCRattribute of the data set to get its description. Understand the variables, their meanings, and how they relate to the medical context (e.g., what each feature like BMI, age, and blood pressure represents in the context of diabetes).
Preparing the data
Rename the
targetcolumn of the todiabetesby using the.rename()method of the DataFrame. Search for its documentation if you are unsure how to use it.Print the DataFrame for visual inspection.
Hints:
If you’re using a local Python installation, you will need to install some packages:
pip install scikit-learn seaborn pingouin. Make sure to install them in thepsy111environmentIf you are using Goolge Colab, you only need to install the pingouin package by creating a code cell at the top of the script and writing:
!pip install pingouin.If you’re using a Jupyter Notebook, make sure to select any of “View as a scrollable element or open in a text editor” at the bottom of the output to see the entire description.
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import statsmodels.formula.api as smf
import pingouin as pg
from sklearn import datasets
# 1. Load the data
diabetes = datasets.load_diabetes(as_frame=True)
diabetes_df = diabetes.frame
print(diabetes.DESCR)
# 2. Preparing the data
diabetes_df.rename(columns={'target': 'diabetes'}, inplace=True)
print(diabetes_df.head())
.. _diabetes_dataset:
Diabetes dataset
----------------
Ten baseline variables, age, sex, body mass index, average blood
pressure, and six blood serum measurements were obtained for each of n =
442 diabetes patients, as well as the response of interest, a
quantitative measure of disease progression one year after baseline.
**Data Set Characteristics:**
:Number of Instances: 442
:Number of Attributes: First 10 columns are numeric predictive values
:Target: Column 11 is a quantitative measure of disease progression one year after baseline
:Attribute Information:
- age age in years
- sex
- bmi body mass index
- bp average blood pressure
- s1 tc, total serum cholesterol
- s2 ldl, low-density lipoproteins
- s3 hdl, high-density lipoproteins
- s4 tch, total cholesterol / HDL
- s5 ltg, possibly log of serum triglycerides level
- s6 glu, blood sugar level
Note: Each of these 10 feature variables have been mean centered and scaled by the standard deviation times the square root of `n_samples` (i.e. the sum of squares of each column totals 1).
Source URL:
https://www4.stat.ncsu.edu/~boos/var.select/diabetes.html
For more information see:
Bradley Efron, Trevor Hastie, Iain Johnstone and Robert Tibshirani (2004) "Least Angle Regression," Annals of Statistics (with discussion), 407-499.
(https://web.stanford.edu/~hastie/Papers/LARS/LeastAngle_2002.pdf)
age sex bmi bp s1 s2 s3 \
0 0.038076 0.050680 0.061696 0.021872 -0.044223 -0.034821 -0.043401
1 -0.001882 -0.044642 -0.051474 -0.026328 -0.008449 -0.019163 0.074412
2 0.085299 0.050680 0.044451 -0.005670 -0.045599 -0.034194 -0.032356
3 -0.089063 -0.044642 -0.011595 -0.036656 0.012191 0.024991 -0.036038
4 0.005383 -0.044642 -0.036385 0.021872 0.003935 0.015596 0.008142
s4 s5 s6 diabetes
0 -0.002592 0.019907 -0.017646 151.0
1 -0.039493 -0.068332 -0.092204 75.0
2 -0.002592 0.002861 -0.025930 141.0
3 0.034309 0.022688 -0.009362 206.0
4 -0.002592 -0.031988 -0.046641 135.0
Exercise 1: Multiple linear regression#
Estimate a multiple linear regression model using
bmi,bp, ands5to predict diabetes progression (diabetes).Estimate a second model with different predictors.
Compare the models. What is their R-squared value? What does it tell you about the performance of the models?
Tip: When working in Jupyter Notebooks, it might make sense to put different models/computations in separate code cells, so they can be evaluated individually and the outputs are easier to read.
model = smf.ols(formula='diabetes ~ bmi + bp + s5', data=diabetes_df)
results = model.fit()
print(results.summary())
OLS Regression Results
==============================================================================
Dep. Variable: diabetes R-squared: 0.480
Model: OLS Adj. R-squared: 0.477
Method: Least Squares F-statistic: 134.8
Date: Wed, 04 Dec 2024 Prob (F-statistic): 7.16e-62
Time: 16:01:54 Log-Likelihood: -2402.6
No. Observations: 442 AIC: 4813.
Df Residuals: 438 BIC: 4830.
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 152.1335 2.653 57.342 0.000 146.919 157.348
bmi 603.0784 64.677 9.324 0.000 475.962 730.194
bp 262.2720 62.962 4.166 0.000 138.527 386.017
s5 543.8712 64.619 8.417 0.000 416.870 670.873
==============================================================================
Omnibus: 9.591 Durbin-Watson: 1.971
Prob(Omnibus): 0.008 Jarque-Bera (JB): 6.859
Skew: 0.183 Prob(JB): 0.0324
Kurtosis: 2.511 Cond. No. 28.3
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
model2 = smf.ols(formula='diabetes ~ sex + s1 + s6', data=diabetes_df)
results2 = model2.fit()
print(results2.summary())
OLS Regression Results
==============================================================================
Dep. Variable: diabetes R-squared: 0.156
Model: OLS Adj. R-squared: 0.150
Method: Least Squares F-statistic: 26.99
Date: Wed, 04 Dec 2024 Prob (F-statistic): 4.93e-16
Time: 16:01:54 Log-Likelihood: -2509.7
No. Observations: 442 AIC: 5027.
Df Residuals: 438 BIC: 5044.
Df Model: 3
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 152.1335 3.380 45.006 0.000 145.490 158.777
sex -56.5320 72.703 -0.778 0.437 -199.421 86.358
s1 156.3080 75.212 2.078 0.038 8.487 304.129
s6 580.0769 76.848 7.548 0.000 429.040 731.114
==============================================================================
Omnibus: 32.093 Durbin-Watson: 1.863
Prob(Omnibus): 0.000 Jarque-Bera (JB): 17.955
Skew: 0.335 Prob(JB): 0.000126
Kurtosis: 2.274 Cond. No. 26.5
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
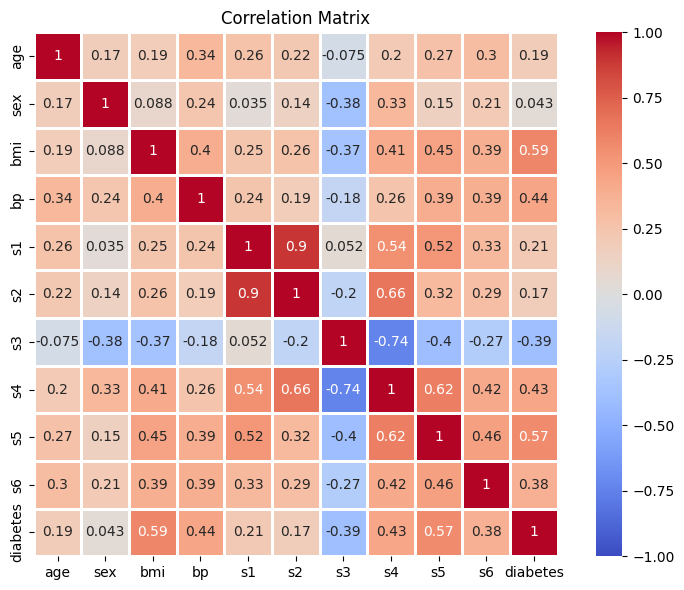
Exercise 2: Correlations#
Correlations
Compute the correlation matrix for all columns in the data
Print the shape of the correlation matrix. What shape does it have, and why?
Visualizing the data
Plot the correlation matrix by using
seaborn’sheatmap()function. The plot should have the following featurees:The cells in the plot should be annotated with the correlation values
The colormap should be
"coolwarm"(it’s a good choice for correlation values)The colorbar should range from
-1to1(because this is the full range correlation values can take)The cells in the plot should be quare (just because it looks nice)
The cells should be separated with lines of width
1(also because it looks nice)
Throug visual inspection, identify the variable that shows the highest correlation (positive or negative) with the target variable (diabetes progression)
# 1. Correlations
correlation_matrix = diabetes_df.corr()
print("Shape of the correlation matrix:", correlation_matrix.shape)
# 2. Visualizing the data
plt.figure(figsize=(8,6))
sns.heatmap(
correlation_matrix,
annot=True,
cmap="coolwarm",
vmin=-1,
vmax=1,
square=True,
linewidths=1
)
plt.title('Correlation Matrix')
plt.tight_layout()
plt.show()
Shape of the correlation matrix: (11, 11)
Exercise 3: Partial Correlation#
Age could be influencing both BMI and diabetes progression. As people age, both their BMI and risk for diabetes may increase, potentially inflating the observed correlation between BMI and diabetes progression. By holding age constant, we can test whether the relationship between BMI and diabetes progression persists independently of age.
Hypothesis:
Null Hypothesis (\(H_0\)): There is no relationship between BMI and diabetes progression after controlling for age.
Alternative Hypothesis (\(H_1\)): There is a relationship between BMI and diabetes progression, even after controlling for age.
Tasks:
Use the
pingouinlibrary to calculate the partial correlation between BMI and diabetes progression, controlling for age.Compare the partial correlation coefficient to the original Pearson correlation coefficient. Did the correlation decrease after accounting for age? What does this suggest about age as a confounding factor?
partial_corr = pg.partial_corr(data=diabetes_df, x='bmi', y='diabetes', covar='age')
pearson_corr = diabetes_df['bmi'].corr(diabetes_df['diabetes'])
print(partial_corr)
print("\nNormal pearson correlation:", pearson_corr)
# Interpretation:
# After controlling for age, the relationship between BMI and diabetes progression persists, though it is slightly weaker.
# This suggests that while age has some influence, BMI remains a significant predictor of diabetes progression.
n r CI95% p-val
pearson 442 0.571553 [0.51, 0.63] 1.309246e-39
Normal pearson correlation: 0.5864501344746885
Voluntary exercise 1: Data wrangling#
We have previously loaded the diabetes dataset with the as_frame=True argument. If we do not specify this argument, the combined DataFrame will not be provided, but rather the data, target, and labels will be returned separately.
Familiarize yourself with the returns of the
load_diabetes()function.What kind of data types are the data, target, and labels?
Manually create the joint DataFrame by combining the data, target, and labels.
Verify that your operations were succesful (e.g. by printing the joint DataFrame).
Hint: There are multiple ways for creating a joint DataFrame. Have a look at section 5.2 if you need a refresher. You could, for example, join two DataFrames/Serier, or you could just add a new column to an existing DataFrame. Feel free to experiment! :)
# Voluntary exercise 1
dataset = datasets.load_diabetes()
# Get observations matrix (X) and target vector (y)
X, y, names = dataset.data, dataset.target, dataset.feature_names
# Option 1: Create a DataFrame and Series object from the numpy arrays and concatenate them
X_df= pd.DataFrame(X, columns=dataset.feature_names)
y_series = pd.Series(y, name="diabetes")
df1 = pd.concat([X_df, y_series], axis=1)
print(df1.head())
print("\n")
# Option 2: Create a DataFrame and append the diabetes column
df2= pd.DataFrame(X, columns=dataset.feature_names)
df2["diabetes"] = y
print(df2.head())
age sex bmi bp s1 s2 s3 \
0 0.038076 0.050680 0.061696 0.021872 -0.044223 -0.034821 -0.043401
1 -0.001882 -0.044642 -0.051474 -0.026328 -0.008449 -0.019163 0.074412
2 0.085299 0.050680 0.044451 -0.005670 -0.045599 -0.034194 -0.032356
3 -0.089063 -0.044642 -0.011595 -0.036656 0.012191 0.024991 -0.036038
4 0.005383 -0.044642 -0.036385 0.021872 0.003935 0.015596 0.008142
s4 s5 s6 diabetes
0 -0.002592 0.019907 -0.017646 151.0
1 -0.039493 -0.068332 -0.092204 75.0
2 -0.002592 0.002861 -0.025930 141.0
3 0.034309 0.022688 -0.009362 206.0
4 -0.002592 -0.031988 -0.046641 135.0
age sex bmi bp s1 s2 s3 \
0 0.038076 0.050680 0.061696 0.021872 -0.044223 -0.034821 -0.043401
1 -0.001882 -0.044642 -0.051474 -0.026328 -0.008449 -0.019163 0.074412
2 0.085299 0.050680 0.044451 -0.005670 -0.045599 -0.034194 -0.032356
3 -0.089063 -0.044642 -0.011595 -0.036656 0.012191 0.024991 -0.036038
4 0.005383 -0.044642 -0.036385 0.021872 0.003935 0.015596 0.008142
s4 s5 s6 diabetes
0 -0.002592 0.019907 -0.017646 151.0
1 -0.039493 -0.068332 -0.092204 75.0
2 -0.002592 0.002861 -0.025930 141.0
3 0.034309 0.022688 -0.009362 206.0
4 -0.002592 -0.031988 -0.046641 135.0

