6.1 Dummy Coding#
Dummy coding enables the comparison of each category of a categorical variable to a reference category, which serves as the baseline for measuring the effects of the other categories. In this coding scheme, the reference category is assigned a value of 0 (corresponding to the intercept), while the dummy variables for the remaining categories are assigned values of either 1 or 0.
To implement dummy coding, we will use a combination of the patsy and statsmodels package, as this provides straightforward and customizable options, particularly for defining the reference category.
First, we will import the essential libraries needed to visualize the data.
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import statsmodels.formula.api as smf
Then we load the data (in this case from a local file) and have a look at it:
df = pd.read_csv("data/alzheimers_data.txt", delimiter='\t').dropna()
print(df.head())
subject sex age WMv WMn WMf SMv SMn SMf \
0 111000 1 29 0.655556 0.604762 0.707143 0.425 0.225 0.333333
1 111001 1 23 0.506667 0.642857 0.846429 0.450 0.100 0.375000
2 111002 1 24 0.602222 0.571429 0.744048 0.650 0.425 0.166667
3 111003 1 33 0.616667 0.692857 0.857143 0.500 0.225 0.250000
4 111004 1 29 0.884444 0.677381 0.871429 0.600 0.200 0.583333
Spd1 Spd2 Spd3 Spd4 gfv gfn gff APOE e4 \
0 2.603213 2.272891 2.324883 2.460446 0.5625 0.3750 0.3750 6.0 0.0
1 2.063279 2.017480 1.904249 1.978650 0.1875 0.4375 0.3750 1.0 1.0
2 2.075107 2.085463 1.902517 1.986161 0.4375 0.6250 0.3125 3.0 1.0
3 2.384937 2.246979 2.157284 2.243270 0.5625 0.5625 0.3125 1.0 1.0
4 1.733822 1.485727 1.963233 1.898097 0.6250 0.4375 0.4375 1.0 1.0
genotype
0 e4/e4
1 e3/e3
2 e2/e3
3 e3/e3
4 e3/e3
We then make sure that the genotype is treated as a categorical variable. For this, we first check its type:
# Since we are working with a pandas dataframe, we can use the
# method ".dtypes" to extract the data type of each column.
data_types = df.dtypes
print(data_types)
subject int64
sex int64
age int64
WMv float64
WMn float64
WMf float64
SMv float64
SMn float64
SMf float64
Spd1 float64
Spd2 float64
Spd3 float64
Spd4 float64
gfv float64
gfn float64
gff float64
APOE float64
e4 float64
genotype object
dtype: object
We see that it is of type object, which is typical for strings. However, for categorical regression, we need to change it to type category using .astype('category'):
df['genotype'] = df['genotype'].astype('category')
print(df["genotype"].dtypes)
category
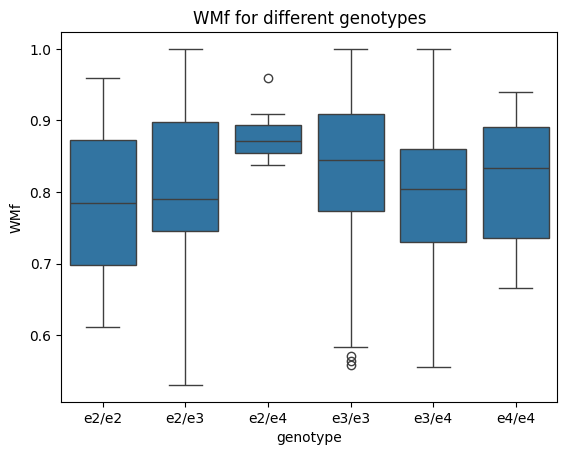
Great, that worked well. We can now proceed to plot the genotypes as individual boxplots against figural working memory ability:WMf. For this we will use seaborn boxplots, as they are easy to use with data frames:
sns.boxplot(x='genotype', y='WMf', data=df)
plt.title("WMf for different genotypes")
plt.show()
We can then perform categorical regression with dummy coding. For this, we use statsmodels combined with the Treatment function from the patsy package:
from patsy.contrasts import Treatment
model = smf.ols('WMf ~ C(genotype, Treatment(reference="e4/e4"))', data=df)
results = model.fit()
print(results.summary())
OLS Regression Results
==============================================================================
Dep. Variable: WMf R-squared: 0.052
Model: OLS Adj. R-squared: 0.032
Method: Least Squares F-statistic: 2.605
Date: Wed, 17 Dec 2025 Prob (F-statistic): 0.0257
Time: 11:07:25 Log-Likelihood: 219.06
No. Observations: 245 AIC: -426.1
Df Residuals: 239 BIC: -405.1
Df Model: 5
Covariance Type: nonrobust
======================================================================================================================
coef std err t P>|t| [0.025 0.975]
----------------------------------------------------------------------------------------------------------------------
Intercept 0.8185 0.032 25.832 0.000 0.756 0.881
C(genotype, Treatment(reference="e4/e4"))[T.e2/e2] -0.0333 0.078 -0.430 0.668 -0.186 0.120
C(genotype, Treatment(reference="e4/e4"))[T.e2/e3] -0.0171 0.036 -0.476 0.634 -0.088 0.053
C(genotype, Treatment(reference="e4/e4"))[T.e2/e4] 0.0610 0.046 1.326 0.186 -0.030 0.152
C(genotype, Treatment(reference="e4/e4"))[T.e3/e3] 0.0166 0.033 0.507 0.613 -0.048 0.081
C(genotype, Treatment(reference="e4/e4"))[T.e3/e4] -0.0325 0.035 -0.928 0.354 -0.102 0.036
==============================================================================
Omnibus: 9.927 Durbin-Watson: 1.820
Prob(Omnibus): 0.007 Jarque-Bera (JB): 10.312
Skew: -0.502 Prob(JB): 0.00577
Kurtosis: 3.026 Cond. No. 16.7
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Interpreting the Output#
When you run the regression WMf ~ C(genotype, Treatment(reference="e4/e4")), the output provides the following key pieces of information:
Intercept:
This is the mean value of
WMffor the reference group (e4/e4in this case).For example, if the intercept is 0.8185, it indicates that the average
WMffor thee4/e4group is 0.8185.
Slopes for Dummy Variables (
C(genotype)[T.<level>]):Each slope represents the difference in the mean value of
WMfbetween the respectivegenotypegroup and the reference group (e4/e4).For example, if
C(genotype)[T.e2/e2]has a coefficient of -0.0333:The mean
WMffor thee2/e2group is 0.0333 less than the mean for thee4/e4group.
Regression Equation:
The regression equation summarizes the relationship between the predictors (
genotypegroups) and the outcome (WMf) by filling in the intercept and the slope specific to each genotype, derived from the output:
Statistical Significance:
The p-values for each coefficient test whether the difference between the respective group and the reference group is statistically significant.
For example:
If
p = 0.668forC(genotype)[T.e2/e2], it indicates that the meanWMffor thee2/e2group is not significantly different from thee4/e4group, as this p-value is above any reasonable significance threshold (e.g., 0.05).
R-squared and Model Fit:
The R-squared value indicates how much of the variation in
WMfis explained by the genotype categories. A higher R-squared value suggests a strong relationship betweengenotypeandWMf.
The Contrast Matrix#
For dummy coding, there is usually no need to manually create dummy variables or to create a contrast matrix, as statsmodels handles this automatically. However, to ensure that we did everything correctly, we can manually create the contrast matrix and have a look at it:
# Get all genotype levels and save them as a list
levels = df['genotype'].cat.categories.tolist()
# Create a Treatment contrast matrix
contrast = Treatment(reference="e4/e4").code_without_intercept(levels)
print("Levels:", levels)
print("Contrast Matrix:\n", contrast.matrix)
Levels: ['e2/e2', 'e2/e3', 'e2/e4', 'e3/e3', 'e3/e4', 'e4/e4']
Contrast Matrix:
[[1. 0. 0. 0. 0.]
[0. 1. 0. 0. 0.]
[0. 0. 1. 0. 0.]
[0. 0. 0. 1. 0.]
[0. 0. 0. 0. 1.]
[0. 0. 0. 0. 0.]]
Summary
In dummy coding, the reference category is assigned a value of 0
You can use
model = smf.ols('WMf ~ C(outcome, Treatment(reference="your reference"))', data=my_data)for dummy coding

