Spline Regression#
For the exercises, we will continue with the same data as in the previous sections. Again, we want to predict wage from age in the Mid-Atlantic Wage Dataset.
# Uncomment the following line when working in Colab
# !pip install ISLP
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import patsy
import statsmodels.api as sm
from ISLP import load_data
df = load_data('Wage')
print(df.head())
year age maritl race education region \
0 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic
1 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic
2 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic
3 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic
4 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic
jobclass health health_ins logwage wage
0 1. Industrial 1. <=Good 2. No 4.318063 75.043154
1 2. Information 2. >=Very Good 2. No 4.255273 70.476020
2 1. Industrial 1. <=Good 1. Yes 4.875061 130.982177
3 2. Information 2. >=Very Good 1. Yes 5.041393 154.685293
4 2. Information 1. <=Good 1. Yes 4.318063 75.043154
Exercise 1: Custom cut points#
Create a regression model to predict
wagefromageby using stepwise functions. However, instead of separating the data into 4 evenly sized bins, this time create custom cut points at age 30, 40, 50, 60, and 70.Print and interpret the model summary
Plot the model
# Fit the model with custom knots
transformed_age = patsy.dmatrix("bs(age, knots=(30,40,50,60,70), degree=0)",
data={"age": df['age']},
return_type='dataframe')
model = sm.OLS(df['wage'], transformed_age)
model_fit = model.fit()
print(model_fit.summary())
# Plot the model
plt.figure(figsize=(10, 6))
xp = np.linspace(df['age'].min(), df['age'].max(), 100)
xp_trans = patsy.dmatrix("bs(xp, knots=(30,40,50,60,70), degree=0)",
data={"xp": xp},
return_type='dataframe')
predictions = model_fit.predict(xp_trans)
sns.scatterplot(data=df, x="age", y="wage", alpha=0.4)
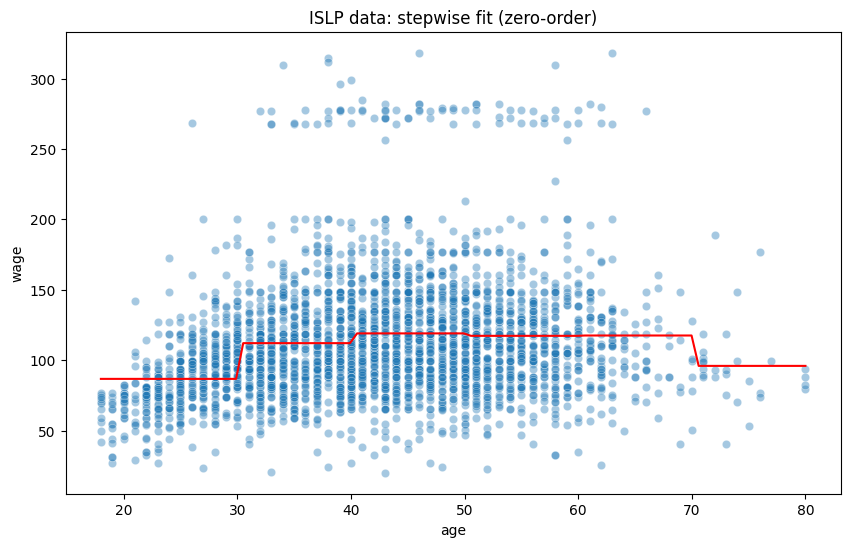
plt.plot(xp, predictions, color='red')
plt.title("ISLP data: stepwise fit (zero-order)");
OLS Regression Results
==============================================================================
Dep. Variable: wage R-squared: 0.070
Model: OLS Adj. R-squared: 0.068
Method: Least Squares F-statistic: 44.90
Date: Wed, 22 Jan 2025 Prob (F-statistic): 7.91e-45
Time: 11:38:41 Log-Likelihood: -15341.
No. Observations: 3000 AIC: 3.069e+04
Df Residuals: 2994 BIC: 3.073e+04
Df Model: 5
Covariance Type: nonrobust
====================================================================================================================
coef std err t P>|t| [0.025 0.975]
--------------------------------------------------------------------------------------------------------------------
Intercept 86.7282 1.903 45.573 0.000 82.997 90.460
bs(age, knots=(30, 40, 50, 60, 70), degree=0)[0] 25.3694 2.395 10.594 0.000 20.674 30.065
bs(age, knots=(30, 40, 50, 60, 70), degree=0)[1] 32.2987 2.315 13.950 0.000 27.759 36.838
bs(age, knots=(30, 40, 50, 60, 70), degree=0)[2] 30.5690 2.481 12.324 0.000 25.705 35.433
bs(age, knots=(30, 40, 50, 60, 70), degree=0)[3] 30.8021 3.591 8.578 0.000 23.762 37.843
bs(age, knots=(30, 40, 50, 60, 70), degree=0)[4] 9.2232 7.070 1.305 0.192 -4.639 23.085
==============================================================================
Omnibus: 1081.976 Durbin-Watson: 1.965
Prob(Omnibus): 0.000 Jarque-Bera (JB): 4742.790
Skew: 1.707 Prob(JB): 0.00
Kurtosis: 8.128 Cond. No. 10.9
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Exercise 2: Higher-order splines#
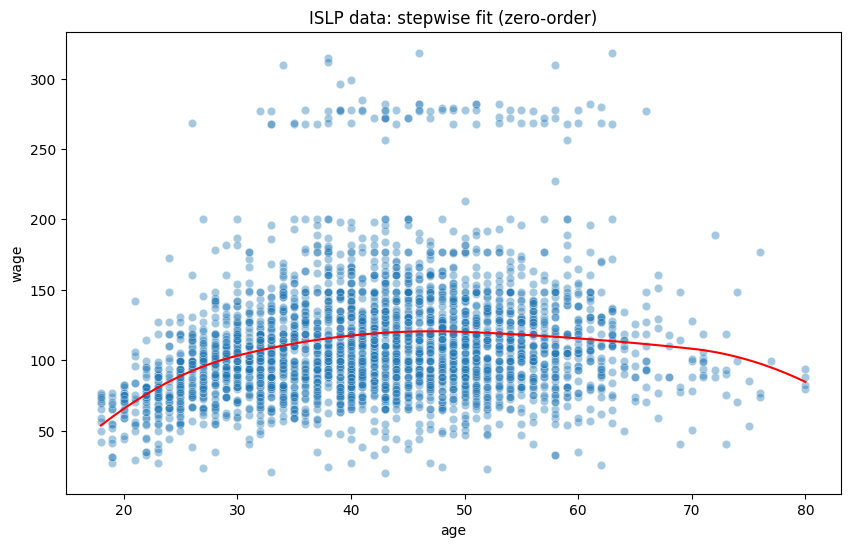
Please fit and plot a second-order spline regression model with cut points at age 30, 50, and 70
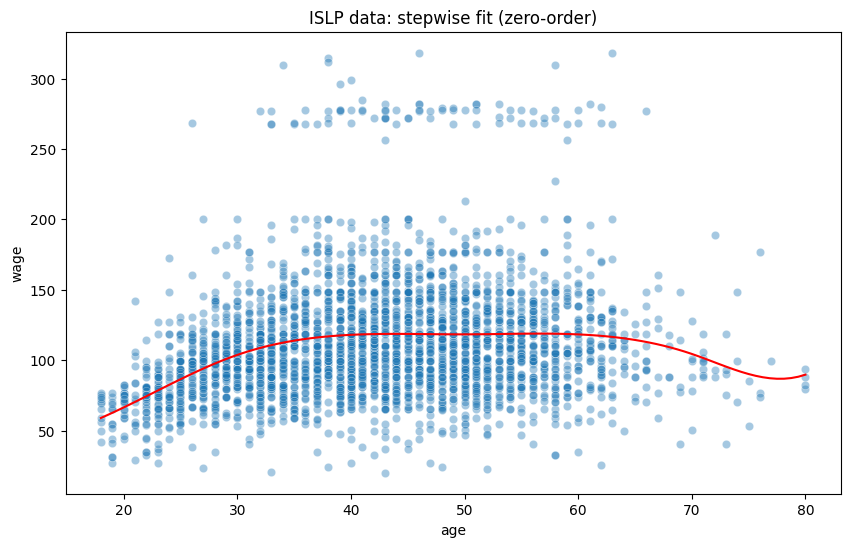
Please fit and plot a third-order spline regression model with cut points at age 30, 50, and 70. Discuss the differences between the models. Does the third-order term significantly improve the model?
# Fit the model with custom knots
transformed_age = patsy.dmatrix("bs(age, knots=(30,50,70), degree=2)",
data={"age": df['age']},
return_type='dataframe')
model = sm.OLS(df['wage'], transformed_age)
model_fit = model.fit()
print(model_fit.summary())
# Plot the model
plt.figure(figsize=(10, 6))
xp = np.linspace(df['age'].min(), df['age'].max(), 100)
xp_trans = patsy.dmatrix("bs(xp, knots=(30,50,70), degree=2)",
data={"xp": xp},
return_type='dataframe')
predictions = model_fit.predict(xp_trans)
sns.scatterplot(data=df, x="age", y="wage", alpha=0.4)
plt.plot(xp, predictions, color='red')
plt.title("ISLP data: stepwise fit (zero-order)");
OLS Regression Results
==============================================================================
Dep. Variable: wage R-squared: 0.086
Model: OLS Adj. R-squared: 0.084
Method: Least Squares F-statistic: 56.07
Date: Wed, 22 Jan 2025 Prob (F-statistic): 7.09e-56
Time: 11:38:42 Log-Likelihood: -15316.
No. Observations: 3000 AIC: 3.064e+04
Df Residuals: 2994 BIC: 3.068e+04
Df Model: 5
Covariance Type: nonrobust
============================================================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------------------------------------
Intercept 53.6414 6.086 8.813 0.000 41.708 65.575
bs(age, knots=(30, 50, 70), degree=2)[0] 37.4841 7.890 4.751 0.000 22.014 52.954
bs(age, knots=(30, 50, 70), degree=2)[1] 69.6654 5.983 11.644 0.000 57.935 81.396
bs(age, knots=(30, 50, 70), degree=2)[2] 63.2010 7.146 8.844 0.000 49.189 77.213
bs(age, knots=(30, 50, 70), degree=2)[3] 50.1480 10.036 4.997 0.000 30.470 69.826
bs(age, knots=(30, 50, 70), degree=2)[4] 30.9407 19.443 1.591 0.112 -7.183 69.064
==============================================================================
Omnibus: 1098.635 Durbin-Watson: 1.961
Prob(Omnibus): 0.000 Jarque-Bera (JB): 4981.584
Skew: 1.723 Prob(JB): 0.00
Kurtosis: 8.290 Cond. No. 32.0
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
# Fit the model with custom knots
transformed_age = patsy.dmatrix("bs(age, knots=(30,50,70), degree=3)",
data={"age": df['age']},
return_type='dataframe')
model = sm.OLS(df['wage'], transformed_age)
model_fit = model.fit()
print(model_fit.summary())
# Plot the model
plt.figure(figsize=(10, 6))
xp = np.linspace(df['age'].min(), df['age'].max(), 100)
xp_trans = patsy.dmatrix("bs(xp, knots=(30,50,70), degree=3)",
data={"xp": xp},
return_type='dataframe')
predictions = model_fit.predict(xp_trans)
sns.scatterplot(data=df, x="age", y="wage", alpha=0.4)
plt.plot(xp, predictions, color='red')
plt.title("ISLP data: stepwise fit (zero-order)");
OLS Regression Results
==============================================================================
Dep. Variable: wage R-squared: 0.087
Model: OLS Adj. R-squared: 0.086
Method: Least Squares F-statistic: 47.77
Date: Wed, 22 Jan 2025 Prob (F-statistic): 3.20e-56
Time: 11:38:42 Log-Likelihood: -15313.
No. Observations: 3000 AIC: 3.064e+04
Df Residuals: 2993 BIC: 3.068e+04
Df Model: 6
Covariance Type: nonrobust
============================================================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------------------------------------
Intercept 58.9573 7.672 7.685 0.000 43.915 73.999
bs(age, knots=(30, 50, 70), degree=3)[0] 14.1773 10.772 1.316 0.188 -6.944 35.299
bs(age, knots=(30, 50, 70), degree=3)[1] 65.9159 7.649 8.618 0.000 50.918 80.914
bs(age, knots=(30, 50, 70), degree=3)[2] 55.1569 9.796 5.630 0.000 35.949 74.365
bs(age, knots=(30, 50, 70), degree=3)[3] 66.0004 9.506 6.943 0.000 47.362 84.639
bs(age, knots=(30, 50, 70), degree=3)[4] 21.4846 15.848 1.356 0.175 -9.589 52.559
bs(age, knots=(30, 50, 70), degree=3)[5] 30.7629 20.860 1.475 0.140 -10.139 71.664
==============================================================================
Omnibus: 1092.629 Durbin-Watson: 1.961
Prob(Omnibus): 0.000 Jarque-Bera (JB): 4914.058
Skew: 1.715 Prob(JB): 0.00
Kurtosis: 8.248 Cond. No. 36.8
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Voluntary exercise 1: Choosing best model#
Now that we fitted multple models, one question remains: Which one do we choose? To decide on that we will use the AIC (note that there are also other measures). Feel free to use whatever cut points you like.
Hints: Try using a loop to achieve this!
You can create a list of formulas ( e.g.,
bs(age, knots=(20,40,60,80), degree=0),bs(age, knots=(20,40,60,80), degree=1), …) and iterate over them.You can use the
.aicattribute of a fitted model to extract the AIC.
formulas = ["bs(age, knots=(20,40,60,80), degree=0)",
"bs(age, knots=(20,40,60,80), degree=1)",
"bs(age, knots=(20,40,60,80), degree=2)",
"bs(age, knots=(20,40,60,80), degree=3)"]
for i, formula in enumerate(formulas):
age_trans = patsy.dmatrix(formula,
data={"age": df['age']},
return_type='dataframe')
print(f"AIC for order {i}:", sm.OLS(df['wage'], age_trans).fit().aic)
AIC for order 0: 30780.420430468923
AIC for order 1: 30647.79526788359
AIC for order 2: 30638.84928413812
AIC for order 3: 30642.64575737064
Voluntary exercise 2: Dynamic plotting#
You might have noticed that sometimes it is hard to see the cutpoints, especially when two bins share very similar estimates (see ). Therefore, it makes sense to highlight the cut points somehow when plotting the models.
Grab a model of your choice and modify the code so that the cut points are marked by black, dashed, vertical lines.
Try to make your code dynamic, meaning it dynamically accepts cut points provided in the
cut_pointslist and automatically fits and plots the model accordingly.Add a legend to the plot and label all lines and and data.
cut_points = (20,40,60,80)
# Fit the model with custom knots
transformed_age = patsy.dmatrix(f"bs(age, knots={str(cut_points)}, degree=2)",
data={"age": df['age']},
return_type='dataframe')
model = sm.OLS(df['wage'], transformed_age)
model_fit = model.fit()
# Plot the model
plt.figure(figsize=(10, 6))
xp = np.linspace(df['age'].min(), df['age'].max(), 100)
xp_trans = patsy.dmatrix("bs(xp, knots=(20,40,60,80), degree=2)",
data={"xp": xp},
return_type='dataframe')
predictions = model_fit.predict(xp_trans)
sns.scatterplot(data=df, x="age", y="wage", alpha=0.4, label="data")
plt.plot(xp, predictions, color='red', label="model")
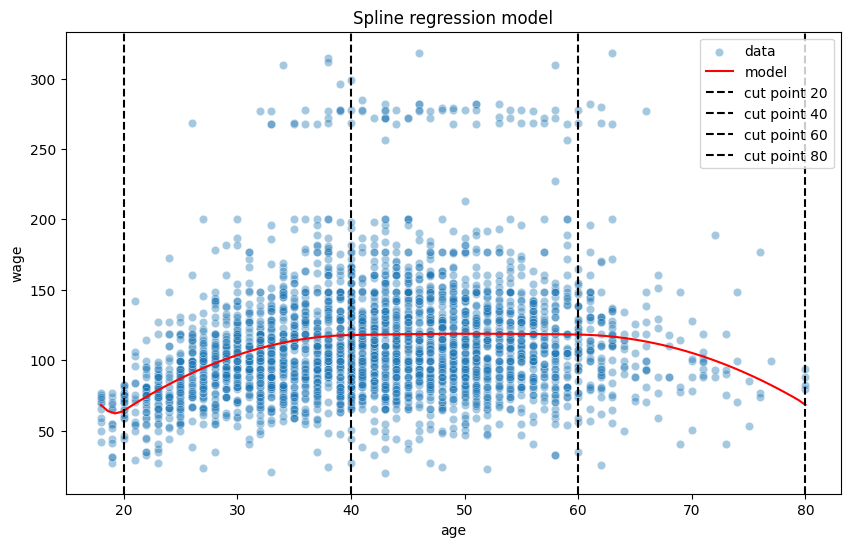
plt.title("Spline regression model");
for cut in cut_points:
plt.axvline(cut, color='black', linestyle='--', label=f"cut point {cut}")
plt.legend();