Logistic Regression#
Exercise 1: Loading the Data#
For today’s exercise we will use the Breast Cancer Wisconsin (Diagnostic). It is a collection of data used for predicting whether a breast tumor is malignant (cancerous) or benign (non-cancerous), containinh information derived from images of breast mass samples obtained through fine needle aspirates.
The dataset consists of 569 samples with 30 features that measure various characteristics of cell nuclei, such as radius, texture, perimeter, and area. Each sample is labeled as either malignant (1) or benign (0).
Please visit the documentation and familiarize yourself with the dataset.
Take an initial look at the features (predictors) and targets (outcomes) through the
.head()method.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix
from ucimlrepo import fetch_ucirepo
# Fetch dataset
breast_cancer_wisconsin_diagnostic = fetch_ucirepo(id=17)
# Data (as pandas dataframes)
X = breast_cancer_wisconsin_diagnostic.data.features
y = breast_cancer_wisconsin_diagnostic.data.targets
# Convert y to a 1D array (this is the required input for the logistic regression model)
y = np.ravel(y)
# Print information
print(breast_cancer_wisconsin_diagnostic.variables)
print(X.head())
print(y)
name role type demographic description units \
0 ID ID Categorical None None None
1 Diagnosis Target Categorical None None None
2 radius1 Feature Continuous None None None
3 texture1 Feature Continuous None None None
4 perimeter1 Feature Continuous None None None
5 area1 Feature Continuous None None None
6 smoothness1 Feature Continuous None None None
7 compactness1 Feature Continuous None None None
8 concavity1 Feature Continuous None None None
9 concave_points1 Feature Continuous None None None
10 symmetry1 Feature Continuous None None None
11 fractal_dimension1 Feature Continuous None None None
12 radius2 Feature Continuous None None None
13 texture2 Feature Continuous None None None
14 perimeter2 Feature Continuous None None None
15 area2 Feature Continuous None None None
16 smoothness2 Feature Continuous None None None
17 compactness2 Feature Continuous None None None
18 concavity2 Feature Continuous None None None
19 concave_points2 Feature Continuous None None None
20 symmetry2 Feature Continuous None None None
21 fractal_dimension2 Feature Continuous None None None
22 radius3 Feature Continuous None None None
23 texture3 Feature Continuous None None None
24 perimeter3 Feature Continuous None None None
25 area3 Feature Continuous None None None
26 smoothness3 Feature Continuous None None None
27 compactness3 Feature Continuous None None None
28 concavity3 Feature Continuous None None None
29 concave_points3 Feature Continuous None None None
30 symmetry3 Feature Continuous None None None
31 fractal_dimension3 Feature Continuous None None None
missing_values
0 no
1 no
2 no
3 no
4 no
5 no
6 no
7 no
8 no
9 no
10 no
11 no
12 no
13 no
14 no
15 no
16 no
17 no
18 no
19 no
20 no
21 no
22 no
23 no
24 no
25 no
26 no
27 no
28 no
29 no
30 no
31 no
radius1 texture1 perimeter1 area1 smoothness1 compactness1 \
0 17.99 10.38 122.80 1001.0 0.11840 0.27760
1 20.57 17.77 132.90 1326.0 0.08474 0.07864
2 19.69 21.25 130.00 1203.0 0.10960 0.15990
3 11.42 20.38 77.58 386.1 0.14250 0.28390
4 20.29 14.34 135.10 1297.0 0.10030 0.13280
concavity1 concave_points1 symmetry1 fractal_dimension1 ... radius3 \
0 0.3001 0.14710 0.2419 0.07871 ... 25.38
1 0.0869 0.07017 0.1812 0.05667 ... 24.99
2 0.1974 0.12790 0.2069 0.05999 ... 23.57
3 0.2414 0.10520 0.2597 0.09744 ... 14.91
4 0.1980 0.10430 0.1809 0.05883 ... 22.54
texture3 perimeter3 area3 smoothness3 compactness3 concavity3 \
0 17.33 184.60 2019.0 0.1622 0.6656 0.7119
1 23.41 158.80 1956.0 0.1238 0.1866 0.2416
2 25.53 152.50 1709.0 0.1444 0.4245 0.4504
3 26.50 98.87 567.7 0.2098 0.8663 0.6869
4 16.67 152.20 1575.0 0.1374 0.2050 0.4000
concave_points3 symmetry3 fractal_dimension3
0 0.2654 0.4601 0.11890
1 0.1860 0.2750 0.08902
2 0.2430 0.3613 0.08758
3 0.2575 0.6638 0.17300
4 0.1625 0.2364 0.07678
[5 rows x 30 columns]
['M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M'
'M' 'B' 'B' 'B' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M'
'M' 'B' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'M'
'M' 'B' 'M' 'M' 'B' 'B' 'B' 'B' 'M' 'B' 'M' 'M' 'B' 'B' 'B' 'B' 'M' 'B'
'M' 'M' 'B' 'M' 'B' 'M' 'M' 'B' 'B' 'B' 'M' 'M' 'B' 'M' 'M' 'M' 'B' 'B'
'B' 'M' 'B' 'B' 'M' 'M' 'B' 'B' 'B' 'M' 'M' 'B' 'B' 'B' 'B' 'M' 'B' 'B'
'M' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'M' 'M' 'B' 'M' 'M' 'B' 'B' 'B'
'M' 'M' 'B' 'M' 'B' 'M' 'M' 'B' 'M' 'M' 'B' 'B' 'M' 'B' 'B' 'M' 'B' 'B'
'B' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'B' 'B' 'M'
'M' 'B' 'M' 'B' 'B' 'M' 'M' 'B' 'B' 'M' 'M' 'B' 'B' 'B' 'B' 'M' 'B' 'B'
'M' 'M' 'M' 'B' 'M' 'B' 'M' 'B' 'B' 'B' 'M' 'B' 'B' 'M' 'M' 'B' 'M' 'M'
'M' 'M' 'B' 'M' 'M' 'M' 'B' 'M' 'B' 'M' 'B' 'B' 'M' 'B' 'M' 'M' 'M' 'M'
'B' 'B' 'M' 'M' 'B' 'B' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'M' 'M' 'B' 'B' 'M'
'B' 'B' 'M' 'M' 'B' 'M' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'M' 'B'
'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'B' 'B' 'B' 'B'
'B' 'B' 'M' 'B' 'M' 'B' 'B' 'M' 'B' 'B' 'M' 'B' 'M' 'M' 'B' 'B' 'B' 'B'
'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'M' 'B' 'M' 'B' 'B' 'B'
'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'B' 'M' 'B' 'M'
'B' 'B' 'B' 'B' 'M' 'M' 'M' 'B' 'B' 'B' 'B' 'M' 'B' 'M' 'B' 'M' 'B' 'B'
'B' 'M' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'M' 'M' 'B' 'B' 'B' 'B' 'B' 'B'
'B' 'B' 'B' 'B' 'B' 'M' 'M' 'B' 'M' 'M' 'M' 'B' 'M' 'M' 'B' 'B' 'B' 'B'
'B' 'M' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'B' 'M' 'B' 'B' 'M' 'M' 'B' 'B'
'B' 'B' 'B' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'B' 'B' 'B'
'M' 'B' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'B'
'M' 'M' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'M' 'B' 'M' 'B' 'B' 'M'
'B' 'M' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'M' 'B' 'B' 'B' 'B' 'B' 'B'
'M' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'B'
'B' 'M' 'B' 'M' 'B' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'M' 'M' 'B' 'M' 'B' 'M'
'B' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'M' 'B' 'M' 'B' 'M' 'M' 'B' 'B' 'B' 'M'
'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'M' 'M' 'B' 'B' 'B'
'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B'
'B' 'B' 'B' 'B' 'M' 'M' 'M' 'M' 'M' 'M' 'B']
Exercise 2: Fitting the prediction model#
Fit a logitic regression model using all predictors for predicting
Get and print the accuracy of the model.
Get and print the confusion matrix for the target variable.
Review the classification report and interpret the results.
Hint: If you get a warning about convergence, try setting max_iter=10000 in the logistic regression class.
model = LogisticRegression(max_iter=10000)
results = model.fit(X, y)
# Get the intercept and coefficients
intercept = results.intercept_
coef = results.coef_
print("Intercept:", intercept)
print("Coefficients:", coef)
# Evaluate the model using predictions
print("Model accuracy:", model.score(X, y))
# Confusion Matrix
conf = confusion_matrix(y, model.predict(X))
print("Confusion matrix:\n", conf)
#classification report
from sklearn.metrics import classification_report
report = classification_report(y, model.predict(X))
print(report)
Intercept: [-27.95056684]
Coefficients: [[-1.01649102 -0.1801684 0.27565655 -0.0226662 0.1788688 0.22074883
0.53685545 0.29603555 0.26639959 0.03046789 0.07816283 -1.25532588
-0.11582457 0.10854792 0.02539334 -0.06767259 0.03651147 0.03822884
0.03627027 -0.0140333 -0.15086497 0.43624862 0.10562901 0.01380557
0.35772193 0.68749004 1.4271106 0.60399598 0.72848145 0.09506939]]
Model accuracy: 0.9578207381370826
Confusion matrix:
[[348 9]
[ 15 197]]
precision recall f1-score support
B 0.96 0.97 0.97 357
M 0.96 0.93 0.94 212
accuracy 0.96 569
macro avg 0.96 0.95 0.95 569
weighted avg 0.96 0.96 0.96 569
Voluntary exercise#
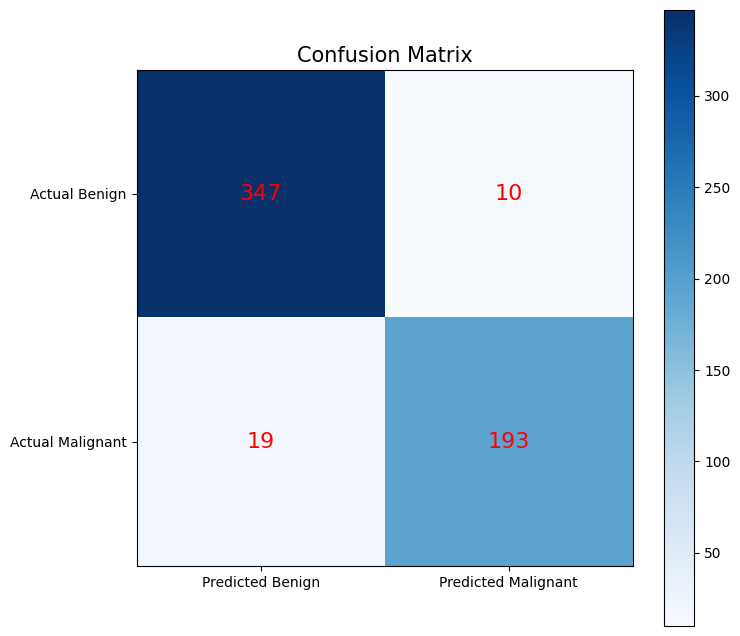
Try to create a custom plot which visualizes the confusion matrix It should contain:
The four squares of the matrix (color coded)
Labels of the actual values in the middle of each square
Labels for all squares
A colorbar
A title
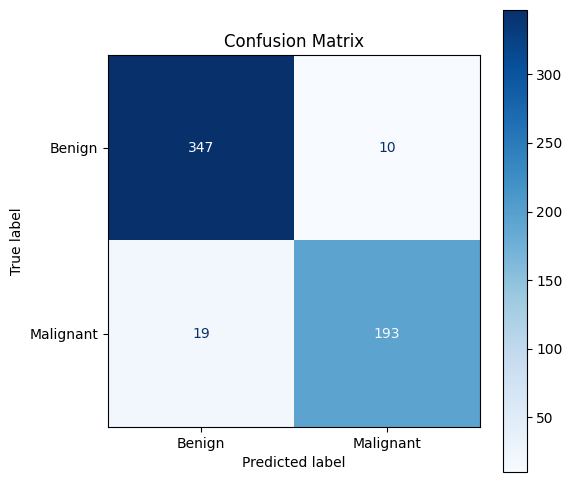
Use
ConfusionMatrixDisplay()from scikit-learn to achieve the same goal (and see that sometimes it makes sense to not re-invent the wheel :))
# 1. Plot a custom confusion matrix
fig, ax = plt.subplots(figsize=(8, 8))
cax = ax.imshow(conf, cmap='Blues')
# labels
ax.xaxis.set(ticks=(0, 1), ticklabels=('Predicted Benign', 'Predicted Malignant'))
ax.yaxis.set(ticks=(0, 1), ticklabels=('Actual Benign', 'Actual Malignant'))
# Annotate the confusion matrix
for i in range(2):
for j in range(2):
ax.text(j, i, conf[i, j], ha='center', va='center', color='red', fontsize=16)
ax.set_title('Confusion Matrix', fontsize=15)
plt.colorbar(cax)
plt.show()
# 2. Using scikit-learn
from sklearn.metrics import ConfusionMatrixDisplay
# Display the confusion matrix using scikit-learn
fig, ax = plt.subplots(figsize=(6, 6))
disp = ConfusionMatrixDisplay(confusion_matrix=conf,
display_labels=["Benign", "Malignant"])
disp.plot(cmap='Blues', ax=ax, colorbar=True)
plt.title("Confusion Matrix")
plt.show()