12.1 Polynomial Regression#
Let’s consider a hypothetical situation in which we want to predict an exam score (0–100%) from the number of hours studied per day. A purely linear model might miss an important “sweet spot,” since studying too many hours can lead to fatigue or burnout. By adding a quadratic term, we can model a peak in performance:
To demostrate this, lets simulate a dataset with two variables study_time and grade:
Show code cell source
import numpy as np
import pandas as pd
# Simulate the data
np.random.seed(69)
study_time = np.linspace(1, 10, 500)
h = 6
k = 80
grades = -(k / (h**2)) * (study_time - h)**2 + k + np.random.normal(0, 8, study_time.shape)
grades = np.clip(grades, 0, 100) # ensure we only have grades between 0 and 100
# Create a DataFrame
df = pd.DataFrame({"study_time": study_time, "grades": grades})
print(df.head())
study_time grades
0 1.000000 31.768501
1 1.018036 20.016187
2 1.036072 34.541517
3 1.054108 20.829142
4 1.072144 13.256199
We can then plot the two variables to check if everything looks as expected:
import seaborn as sns
import matplotlib.pyplot as plt
fig, ax = plt.subplots(figsize=(8,5))
sns.scatterplot(data=df, x="study_time", y="grades", alpha=0.6, ax=ax)
ax.set(xlabel="Learn [h]",
ylabel="Grade [%]",
title="Scatter Plot: Study-time vs. Grade");
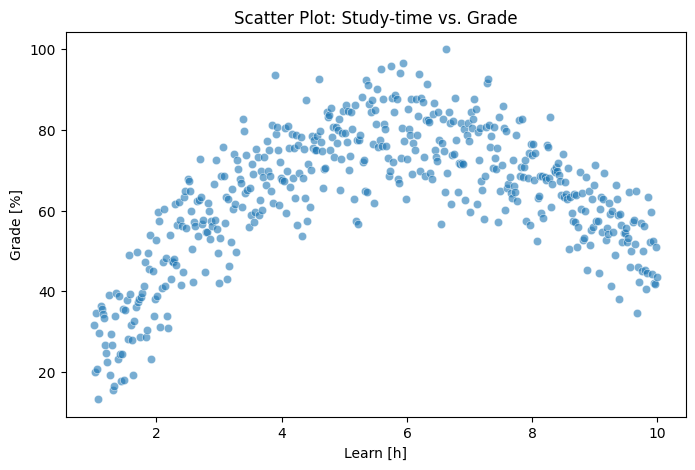
That seems to work! We can clearly see the non-linear component is present in our data. We will now proceed to first fit a linear and then a polynomial model to this data. For this, we will use the statsmodels and sklearn packages.
Fitting polynomial models#
To begin with, lets start with a first order polynomial model. You will then see how easy it is to extend this to as many orders as you like :)
First order polynomial model#
To creare a polynomial model, we first need to create polynomial features:
import statsmodels.api as sm
from sklearn.preprocessing import PolynomialFeatures
polynomial_features_p1 = PolynomialFeatures(degree=1, include_bias=True)
study_time_p1 = polynomial_features_p1.fit_transform(study_time.reshape(-1, 1))
What are polynomial features?
In a standard linear regression, our model has the form
However, this assumes a linear relationship between \(x\) (e.g., study time) and \(y\) (e.g., grades). If we suspect a non-linear relationship, we can augment our single feature \(x\) with additional powers of \(x\) (e.g., \(x^2, x^3, \dots\)). This creates a polynomial model, for instance:
Why do we need to transform \(x\) into polynomial features?
Ordinary Least Squares (OLS) regression, by itself, fits linear relationships between predictors and the outcome. To enable OLS to fit a polynomial curve, we transform each original predictor into several “polynomial features” (e.g., \(x^1, x^2, x^3 \ldots\)) and then feed these new features into the linear regression model. Under the hood, the regression is still linear in terms of these transformed features, but effectively it’s fitting a polynomial in terms of the original \(x\).
Using PolynomialFeatures(degree=1, include_bias=True)
degree=1 means we want to create polynomial features up to (and including) the first power. include_bias=True means a column of all 1’s (the “bias term”) will be added automatically, corresponding to the intercept \(\beta_0\).
For degree=1, the transformation looks like:
So you end up with two columns: one for the intercept (all 1’s) and one for the original \(x\) values.
Fitting and transforming
fit_transform(study_time.reshape(-1, 1)) does two things:
It reshapes
study_timefrom shape(n,)into a 2D array of shape(n,1)by using.reshape(-1, 1). This is the expected input for the sklearn library.It applies the transformation to the original data, producing a 2D array of shape
n, 2(fordegree=1), where \(n\) is the number of data points. The first column ofstudy_time_p1is all 1’s (intercept), and the second column is the original study times becausedegree=1is technically the same as a standard linear regression. However, if you later decide to use higher degrees, you will get columns for \(x^1,x^2, \dots x^n\). That’s when you can capture curved relationships in your model.
With the features created, we can then use the standard sm.OLS() approach to create and fit the model:
# Fit the model
model_linear = sm.OLS(grades, study_time_p1)
model_linear_fit = model_linear.fit()
# Get model predictions and residuals
linear_predictions = model_linear_fit.predict(study_time_p1)
linear_residuals = model_linear_fit.resid
Now we can visualize the model and its residuals:
fig, ax = plt.subplots(1, 2, figsize=(8,4))
sns.scatterplot(data=df, x="study_time", y="grades", color='blue', alpha=0.5, ax=ax[0])
ax[0].plot(study_time, linear_predictions, color='red', linewidth=2)
ax[0].set_title('Linear Regression')
sns.scatterplot(data=df, x="study_time", y=linear_residuals, color='red', alpha=0.5, ax=ax[1])
bottom, top = ax[1].get_ylim() # Get y-axis lower and upper limits
ax[1].axhline(0, linestyle='--')
ax[1].set_title('Residuals');
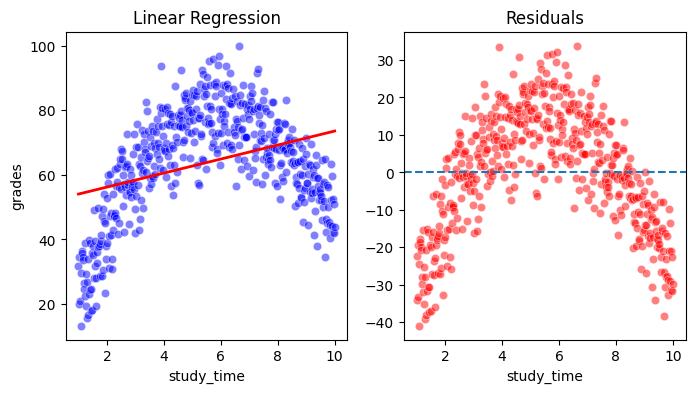
From the upper plot one can already see that whilst there being a linear trend present in the data, the model underestimates the complexitiy of the relationship. Looking at the residuals, it becomes clear that once the strong positive linear trend in the data has been removed, the curvilinearity stands out! The residuals are systematically related to the value of \(X\): below zero for low and high values of \(X\), and above zero for moderate values of \(X\). This is the graphical diagnosis for the existence of a non-linear relationship, higher than degree “1”.
Second order polynomial model#
To improve model fit, lets inlcude a second order polynomials. The procedure is the same as before, except we now use degree=2 for our features:
# Transform study_time
polynomial_features_p2 = PolynomialFeatures(degree=2, include_bias=True)
study_time_p2 = polynomial_features_p2.fit_transform(study_time.reshape(-1, 1))
# Fit the model
model_quadratic = sm.OLS(grades, study_time_p2)
model_quadratic_fit = model_quadratic.fit()
# Get model predictions and residuals
quadratic_predictions = model_quadratic_fit.predict(study_time_p2)
quadratic_residuals = model_quadratic_fit.resid
Lets also plot our new model and its residuals:
fig, ax = plt.subplots(1, 2, figsize=(8,4))
sns.scatterplot(data=df, x="study_time", y="grades", color='blue', alpha=0.5, ax=ax[0])
ax[0].plot(study_time, quadratic_predictions, color='red', linewidth=2)
ax[0].set_title('Quadratic Regression')
sns.scatterplot(data=df, x="study_time", y=quadratic_residuals, color='red', alpha=0.5, ax=ax[1])
ax[1].set_ylim(bottom, top) # Set y-axis lower and upper limits
ax[1].axhline(0, linestyle='--')
ax[1].set_title('Residuals');
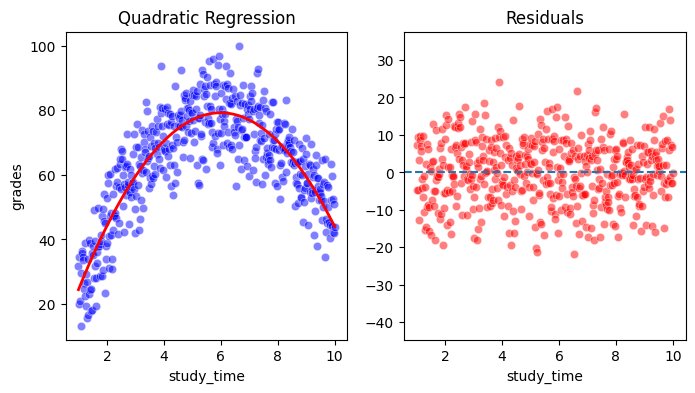
We can already see that the model fits the data much better. Also, the residuals are smaller and not dependent on \(X\).
Interpretation#
The interpretation of the model results is similar to that for normal linear models, except that we now have estimates for the linear and quadratic terms:
print(model_quadratic_fit.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.750
Model: OLS Adj. R-squared: 0.749
Method: Least Squares F-statistic: 744.5
Date: Wed, 09 Apr 2025 Prob (F-statistic): 3.14e-150
Time: 08:53:24 Log-Likelihood: -1771.1
No. Observations: 500 AIC: 3548.
Df Residuals: 497 BIC: 3561.
Df Model: 2
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 0.2520 1.696 0.149 0.882 -3.080 3.584
x1 26.3391 0.695 37.874 0.000 24.973 27.705
x2 -2.1972 0.062 -35.524 0.000 -2.319 -2.076
==============================================================================
Omnibus: 4.382 Durbin-Watson: 2.014
Prob(Omnibus): 0.112 Jarque-Bera (JB): 3.932
Skew: -0.149 Prob(JB): 0.140
Kurtosis: 2.685 Cond. No. 231.
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Coefficients
Intercept (
const): Close to zero (not significant).Linear term (
x1): Positive and highly significant.Quadratic term (
x2): Negative and highly significant, indicating an inverted U-shaped relationship.
Model Fit
R-squared = 0.750: 75% of the variance ingradeis explained.A negative quadratic term means the model predicts an initial increase in grade as study time increases, followed by a decrease past a certain point.
To further evaluate the model, lets also look at the model fit from the linear model:
print(model_linear_fit.summary())
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.114
Model: OLS Adj. R-squared: 0.113
Method: Least Squares F-statistic: 64.28
Date: Wed, 09 Apr 2025 Prob (F-statistic): 7.76e-15
Time: 08:53:24 Log-Likelihood: -2087.1
No. Observations: 500 AIC: 4178.
Df Residuals: 498 BIC: 4187.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 51.8266 1.647 31.468 0.000 48.591 55.062
x1 2.1700 0.271 8.017 0.000 1.638 2.702
==============================================================================
Omnibus: 20.220 Durbin-Watson: 0.569
Prob(Omnibus): 0.000 Jarque-Bera (JB): 15.799
Skew: -0.343 Prob(JB): 0.000371
Kurtosis: 2.463 Cond. No. 14.5
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
We can observe the following:
The quadratic model explains much more variance (75% vs. 11.4%) and provides a better fit according to AIC/BIC.
The negative quadratic term suggests that once study time goes beyond a certain point, additional hours may lead to diminishing or even negative returns on grades (the “inverted U” shape).
Therefore, having a quadratic term improves the model substantially and gives us a more nuanced picture of how study time relates to grades.