Multilevel Models#
Multilevel models, also called linear mixed models (LMMs), are a statistical approach to simultaneously model predictors at different levels of data. These models help account for variability within and between nested groups, such as individuals within clusters or organizations. Multilevel regression is particularly useful for analyzing nested sources of variability, allowing researchers to explore questions about relationships both within and between these levels.
A Practical Example#
Imagine we have data from patients in three different hospitals, and we aim to predict “will to live” (\(Y\)) based on “symptom severity” (\(X\)). At first glance, the data may suggest a positive relationship between “will to live” and “symptom severity”: the more severe the symptoms, the higher the will to live. This finding might appear counterintuitive.
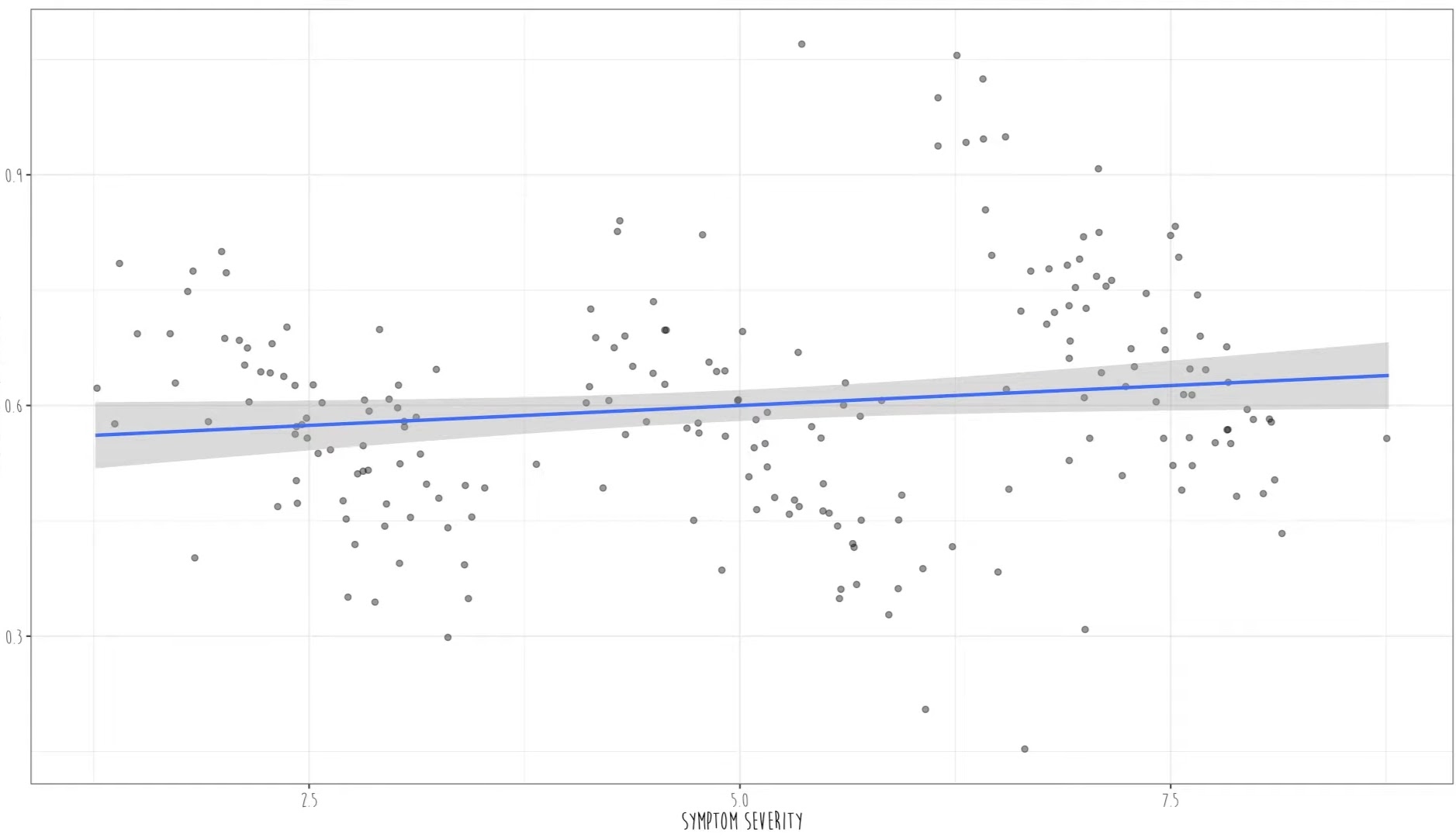
Fig. 5 Screenshot taken from Quant Psych (Youtube)#
When we color-code the data points by hospital, however, a different pattern emerges. Within each hospital, the relationship between “will to live” and “symptom severity” is negative - as symptom severity increases, the will to live decreases, which is a more intuitive result.
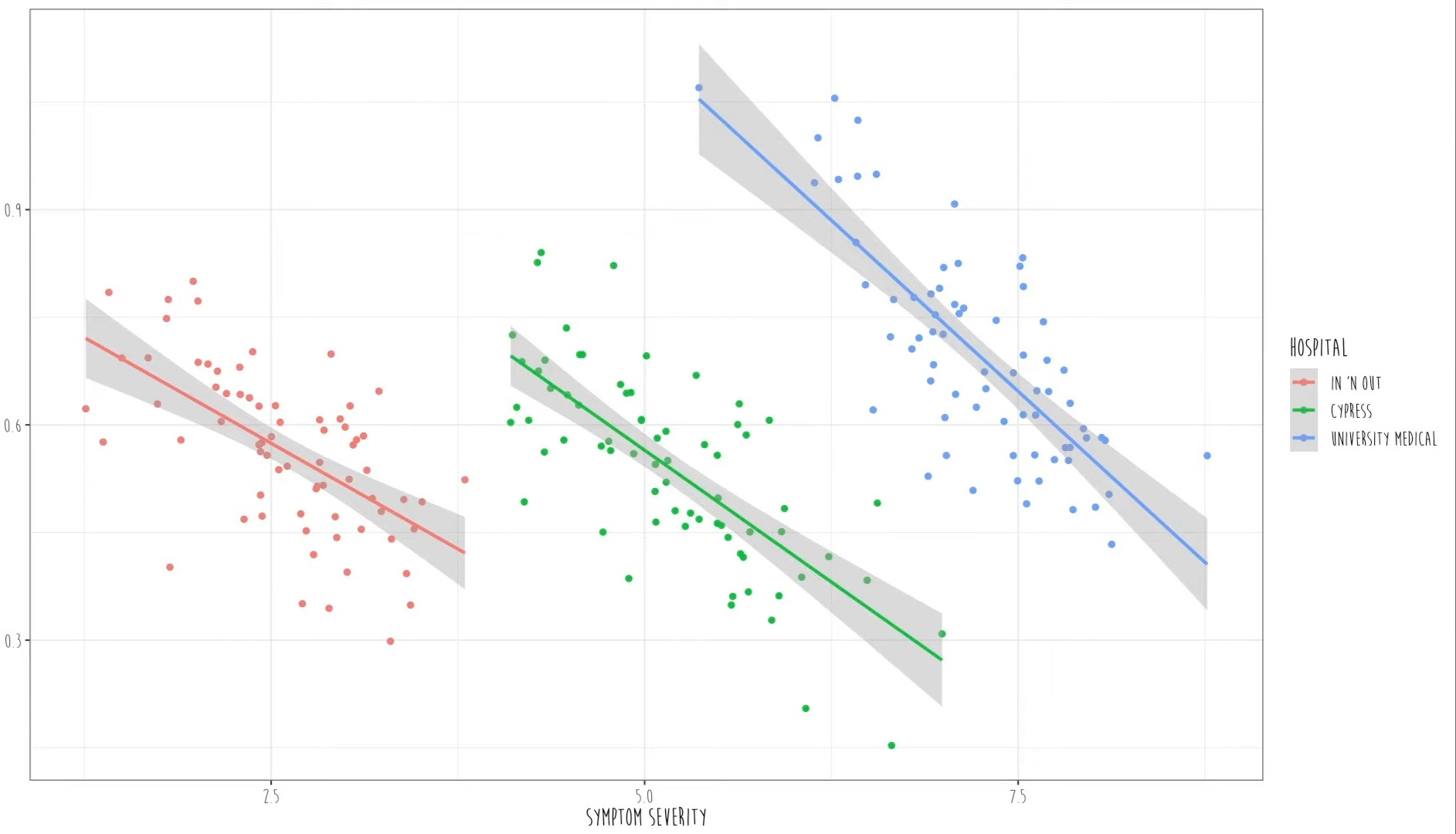
Fig. 6 Screenshot taken from Quant Psych (Youtube)#
If we ignore the clustering variable “hospital,” we risk being misled by the data. This is because data points within a single hospital tend to influence one another. For example:
Blue Hospital: This hospital might exclusively treat severe cases. However, it could have highly skilled psychologists who boost their patients’ “will to live” scores.
Red Hospital: This hospital might primarily admit mild cases and provides lower-quality care, leading to generally lower “will-to-live” scores.
In this scenario, the variable “staff quality” could explain the differences in “will to live” between hospitals. Here, hospitals are level-2 units, and patients are level-1 units. Variables like “staff quality” that explain differences between level-2 units are called level-2 variables.
Even within clusters (hospitals), there is a person-to-person variability. For instance:
Some patients with less severe symptoms report a very low will to live.
Others with more severe symptoms report a relatively high will to live.
This variability within hospitals is at level 1 and could be explained by factors like individual “resilience.” Variables that explain differences between individuals (level-1 units) are referred to as level-1 variables.
Summary
Multilevel models account for nested data structures, such as patients nested within hospitals
Ignoring clustering variables can lead to misleading conclusions, as relationships may differ within and between clusters
Multilevel models allow researchers to distinguish between level-1 (within-cluster) and level-2 (between-cluster) variability, providing deeper insights into the data

