12.2 Centering Predictors

A “meaningful zero” in a predictor variable means that the zero point of this variable has a substantive interpretation, in contrast to e.g. an age of 0 if your sample only contains adults. In polynomial regression, a meaningful zero is especially useful as it improves the interpretation of lower-order coefficients.

Centering thus:

• Simplifies the interpretation: When you center the predictor, the interpretation of lower-order terms becomes simpler. For example, in a centered quadratic model, the linear coefficient now tells you the rate of change at the mean of the predictor, rather than at zero, which might not be a meaningful or sensible point.

Example

Consider a simple quadratic regression model:

\[\hat{y} = \beta_0 + \beta_1 \cdot x + \beta_2 \cdot x^2\]

Without centering, \(\beta_1\) is interpreted as the rate of change of \(y\) with respect to \(x\) when \(x\) is zero. If zero is not meaningful (e.g., if \(x\) is the age in a sample of only adults), this interpretation doesn’t make much practical sense. With centering, \(\beta_1\) is interpreted as the rate of change of \(y\) with respect to \(x\) when \(x\) is at its mean, which can be helpful.

We can center study_time by simply substracting its mean:

Note:

In our example, we have a meaningful 0, since 𝑥 = 0 represents 0 hours of study per day, so centering would not be strictly necessary. However, one could argue that we could improve on it, since very few students study exactly 0 hours. After centering, the linear coefficient tells us the slope of exam performance at mean study time.

import numpy as np
import seaborn as sns
import statsmodels.api as sm
from matplotlib import pyplot as plt
from sklearn.preprocessing import PolynomialFeatures

# Simulate the data
np.random.seed(69)
study_time = np.linspace(1, 10, 500)
h = 6
k = 80
grades = -(k / (h**2)) * (study_time - h)**2 + k + np.random.normal(0, 8, study_time.shape)

# Center study_time
study_time_centered = study_time - np.mean(study_time)

# Create polynomial features
poly_features = PolynomialFeatures(degree=2, include_bias=True)
study_time_centered_features = poly_features.fit_transform(study_time_centered.reshape(-1, 1))

# Fit the model
model_fit = sm.OLS(grades, study_time_centered_features).fit()
predictions = model_fit.predict(study_time_centered_features)
residuals = model_fit.resid

# Plot the residuals
fig, ax = plt.subplots(1, 2, figsize=(8,4))

sns.scatterplot(x=study_time_centered, y=grades, color='blue', alpha=0.5, ax=ax[0])
ax[0].plot(study_time_centered, predictions, color='red', linewidth=2)
ax[0].set_title('Polynomial Regression')

sns.scatterplot(x=study_time_centered, y=residuals, color='red', alpha=0.5, ax=ax[1])
ax[1].axhline(0, linestyle='--')
ax[1].set_title('Residuals');

# Print summary
print(model_fit.summary())

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.750
Model:                            OLS   Adj. R-squared:                  0.749
Method:                 Least Squares   F-statistic:                     744.2
Date:                Wed, 09 Apr 2025   Prob (F-statistic):          3.42e-150
Time:                        08:53:27   Log-Likelihood:                -1771.2
No. Observations:                 500   AIC:                             3548.
Df Residuals:                     497   BIC:                             3561.
Df Model:                           2                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
const         78.6538      0.563    139.821      0.000      77.549      79.759
x1             2.1701      0.144     15.064      0.000       1.887       2.453
x2            -2.1973      0.062    -35.516      0.000      -2.319      -2.076
==============================================================================
Omnibus:                        4.231   Durbin-Watson:                   2.015
Prob(Omnibus):                  0.121   Jarque-Bera (JB):                3.817
Skew:                          -0.147   Prob(JB):                        0.148
Kurtosis:                       2.690   Cond. No.                         13.7
==============================================================================

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

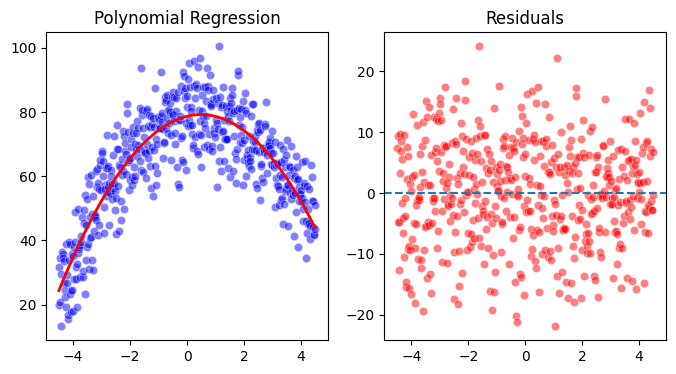
Interpretation

• The expected grade for an average study_time is 78.65 (in a scale between 0 and 100).

• The linear regression of Y on X at the mean of X (which is now 0) is 2.17. The positive coefficient tells us that at the mean of study_time, grade is still increasing. This value also indicates the average linear slope of the regression of Y on X in the quadratic equation.

• The negative quadratic coefficient tells us that the function has an inverted-U shape.

• The variance explained by the model stays the same.